Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O):
AB là tiếp tuyến; B là tiếp điểm (gt). \(\Rightarrow\widehat{ABO}=90^o.\)
AC là tiếp tuyến; C là tiếp điểm (gt). \(\Rightarrow\widehat{ACO}=90^o.\)
\(\Rightarrow\) 4 điểm A, B, O, C cùng thuộc một đường tròn đường kính AO.
b) Xét (O):
\(\widehat{ACD}=\widehat{AEC}\) (Góc tạo bởi tia tiếp tuyến và dây; góc nội tiếp cùng chắn \(\stackrel\frown{CD}\)).
Xét \(\Delta ACD\) và \(\Delta AEC:\)
\(\widehat{ACD}=\widehat{AEC}\left(cmt\right).\)
\(\widehat{CAD}chung.\)
\(\Rightarrow\Delta ACD=\Delta AEC\left(g-g\right).\)
\(\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}.\\ \Rightarrow AC^2=AD.AE.\)

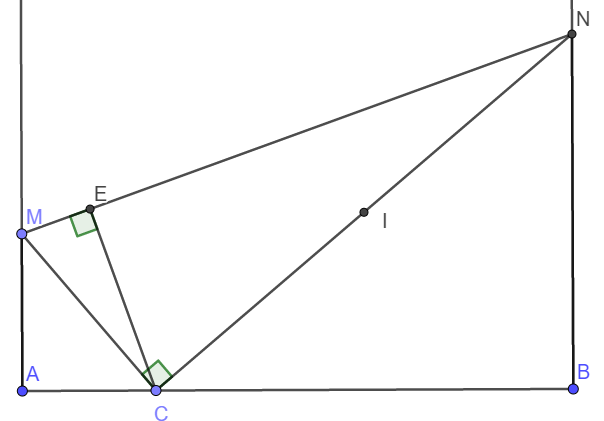
a) Tứ giác CENB có \(\widehat{CEN}=\widehat{CBN}=90^o\) nên bốn điểm B, C, E, N cùng thuộc đường tròn đường kính CN.
b) Ta có ngay \(\Delta MAC\sim\Delta CBN\left(g-g\right)\Rightarrow\frac{AM}{BC}=\frac{AC}{NB}\Rightarrow AM.BN=AC.BC\)
c) Ta có \(S_{AMNB}=\frac{\left(AM+BN\right).AB}{2}\)
Do AB, AM không đổi nên SAMNB lớn nhất khi và chỉ khi BN lớn nhất.
\(BN=\frac{AC.CB}{AM}\le\frac{\frac{\left(AC+CB\right)^2}{4}}{AM}=\frac{AB^2}{4AM}\)
Dấu bằng xảy ra khi \(AC=CB\) hay C là trung điểm AB.

DA*DP=DB*DC
=>DA/DC=DB/DP
=>ΔDAB đồng dạng với ΔDCP
=>góc BAD=góc PCD
=>ABPC nội tiếp
y'y B D A C M F E
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE
a) b) Đưa các đẳng thức về dạng đẳng thức của các tỉ số và áp dụng để chứng minh các cặp tam giác đồng dạng.
c) Từ hai phần a và b, ta suy ra \widehat{CAM}=\widehat{MFE}CAM=MFE.