Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa lại đề : A < 90*
a, Chứng minh
\(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
\(\RightarrowĐPCM\)
b, CM được :
\(\widehat{ADE}\)\(=\)\(\widehat{ACB}\)\(=\)\(\frac{180'-\widehat{BAC}}{2}\)
\(\Rightarrow DE//BC\)
c, CM được : \(\widehat{IBC}=\widehat{ICB}\)
\(\RightarrowĐPCM\)
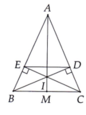
d, Gọi M là giao điểm của AI và BC ,
CM được AI là tia phân giác của góc \(\widehat{BAC}\), từ đó \(\widehat{AMB}\)\(=90'\)
\(\RightarrowĐPCM\)

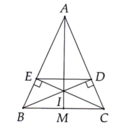
a: Xét ΔADB vuông tại Dvà ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>AD=AE
b: Xét ΔAEI vuông tại E và ΔADI vuông tại D có
AI chung
AE=AD
=>ΔAEI=ΔADI
=>góc EAI=góc DAI
=>AI là phân giác của góc BAC
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
d: AB=AC
IB=IC
=>AI là trung trực của BC
=>A,I,M thẳng hàng

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC

a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC(ΔABC cân tại A)
\(\widehat{BAD}\) chung
Do đó: ΔABD=ΔACE(cạnh huyền-góc nhọn)
Suy ra: BD=CE(hai cạnh tương ứng)
b) Ta có: ΔABD=ΔACE(cmt)
nên AD=AE(hai cạnh tương ứng)
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)