Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét ΔECB và ΔDBC, ta có :
EC = BD (gt)
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
BC là cạnh chung
=> ΔECB = ΔDBC (c.g.c)
=> \(\widehat{GBC}=\widehat{GCB}\) (2 góc tương ứng)
vì ΔGBC có \(\widehat{GBC}=\widehat{GCB}\) nên ⇒ ΔGBC là một tam giác cân (cân tại G)

a: G là trọng tâm
=>BG=2/3BD; CG=2/3CE
=>BG=CG
=>DG=GE
b: Xet ΔEBC và ΔDCB có
BC chung
góc ECB=góc DBC
EC=BD
=>ΔEBC=ΔDCB
=>góc ABC=góc ACB
=>ΔACB cân tại A

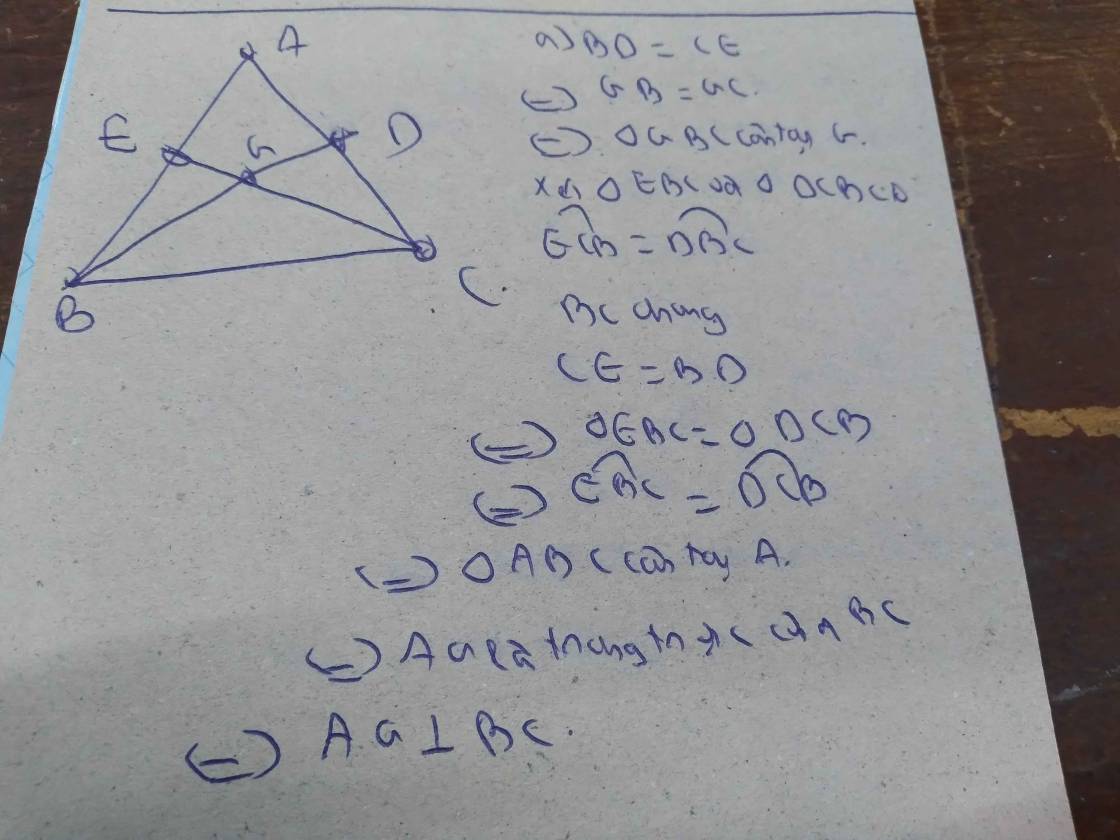
a: Xét ΔEBC và ΔDCB co
EB=DC
góc EBC=góc DCB
CB chung
=>ΔEBC=ΔDCB
=>EC=BD; góc GBC=góc GCB
=>GB=GC
=>GE=GD
=>ΔGED cân tại G
b: BD+CE=3/2(BG+CG)>3/2BC

Xét ΔABD và ΔACE có
AB=AC
góc BAD chung
AD=AE
=>ΔABD=ΔACE
Sửa đề: ΔGBC cân tại G
Xét ΔEBC và ΔDCB có
EB=DC
góc EBC=góc DCB
BC chung
=>ΔEBC=ΔDCB
=>góc GBC=góc GCB
=>ΔGBC cân tại G


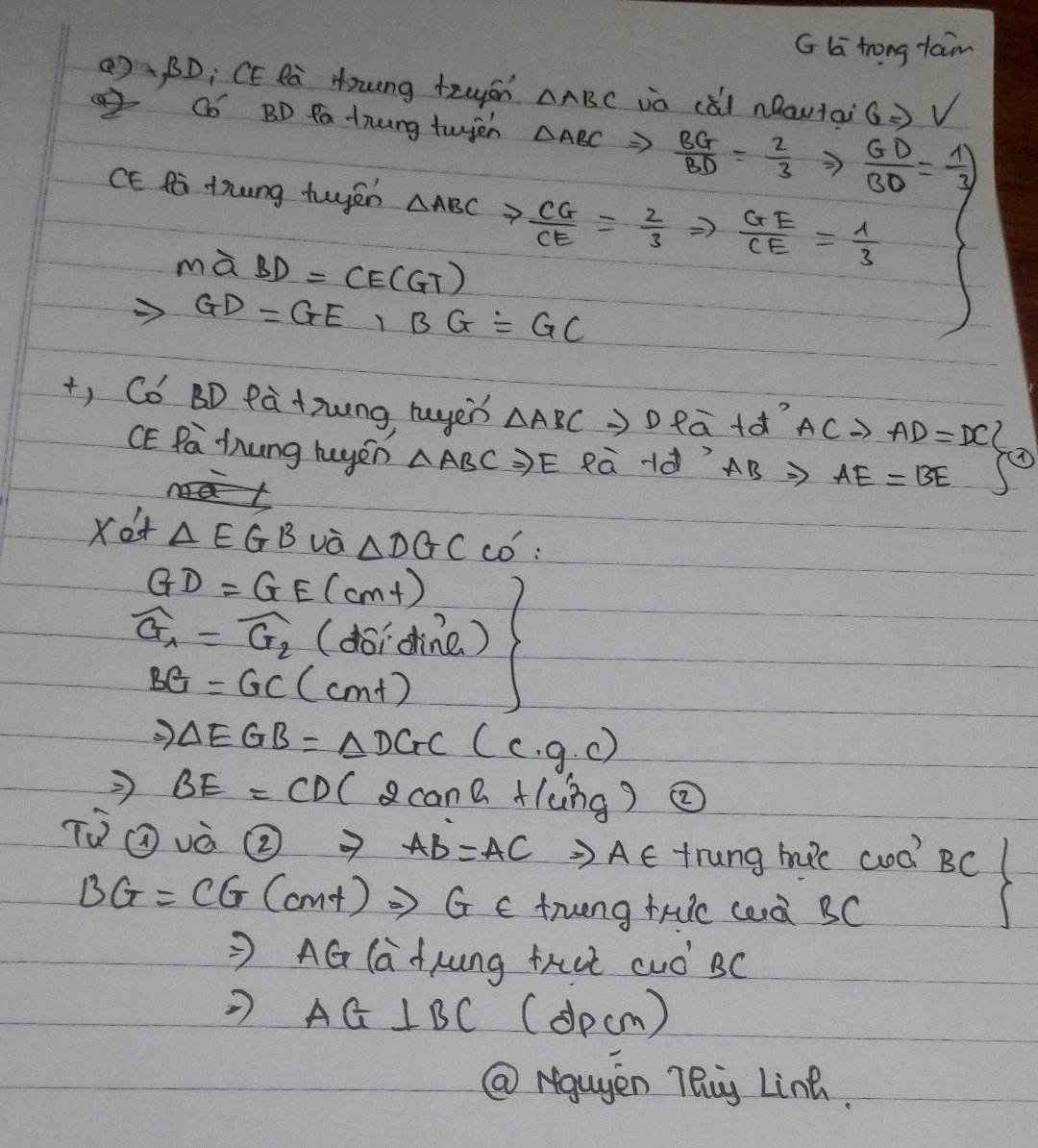
DG+EG=1/3BD+1/3CE=2/3BD=BG>1/2BC