Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác ABC cân tại A, ta có:
góc B = góc C ( tính chất tam giác cân )
Xét tam giác ABC ta có:
góc A + góc B + góc C = 180 độ (định lý tổng ba góc trong tam giác)
mà góc A= 120 độ (gt) , góc B = góc C ( cmt)
-> 120 độ + 2B = 180 độ
-> 2B = 180-120=60 độ
-> B=60 :2=30 độ.
Vì trong tam giác cân đường phân giác cũng đồng thời là đường cao
-> AD vuông góc với BC
vì AD song song với BE
mà góc ADC và góc EBC là 2 góc đồng vị
-> ADC = EBC -> EBC = 90 độ
Ta có : EBC = ABC + ABE
mà EBC = 90 độ , ABC=30 độ
-> ABE = 90-30=60 độ
Ta có : BAE + BAC = 180 độ ( 2 góc kề bù )
mà BAC = 120 đô
-> BAE = 180-120 =60 độ
XÉT tam giác ABE có góc BAE = 60 độ , góc ABE = 60độ
-> tam giác ABE đều
a, Xét tam giác ABC cân tại A, ta có:
góc B = góc C ( tính chất tam giác cân )
Xét tam giác ABC ta có:
góc A + góc B + góc C = 180 độ (định lý tổng ba góc trong tam giác)
mà góc A= 120 độ (gt) , góc B = góc C ( cmt)
-> 120 độ + 2B = 180 độ
-> 2B = 180-120=60 độ
-> B=60 :2=30 độ.
Vì trong tam giác cân đường phân giác cũng đồng thời là đường cao
-> AD vuông góc với BC
vì AD song song với BE
mà góc ADC và góc EBC là 2 góc đồng vị
-> ADC = EBC -> EBC = 90 độ
Ta có : EBC = ABC + ABE
mà EBC = 90 độ , ABC=30 độ
-> ABE = 90-30=60 độ
Ta có : BAE + BAC = 180 độ ( 2 góc kề bù )
mà BAC = 120 đô
-> BAE = 180-120 =60 độ
XÉT tam giác ABE có góc BAE = 60 độ , góc ABE = 60độ
-> tam giác ABE đều

bạn tự vẽ hình nhé
a) ta có:
EAB + CAB = 1800 ( 2 góc kề bù )
EAB + 1200 = 1800
=> EAB = 1800 - 1200 = 600 (1)
vì: EB // AD
=> EBA = BAD = 120/2 = 600
mà EAB + ABE + BEA = 1800
=> 600 + 600 + BEA = 1800
=> BEA = 1800 - 600 - 600 = 600
=> TAM GIÁC ABE ĐỀU (CÓ 3 GÓC = 600) (đpcm)

a, Có BE // AD (gt)
=> góc EBA = góc BAD (2 góc so le trong)
=> góc EBA = góc BAD = 1/2 góc BAC = 120o/2 = 60o (1)
Tam giác BEA có: góc BEA + góc EBA = góc BAC (t/c góc ngoài)
=> góc BEA = góc BAC - góc EBA = 120o - 60o = 60o (2)
Từ (1)(2) => Tam giác BEA cân
Mà tam giác BEA có : góc EBA = 60o (c/m trên)
=> tam giác BEA đều
b, Tam giác ABC cân (gt) => góc ABc = góc ACB = 90o - góc BAC/2 = 90o - 120o/2 = 30o
Tam giác BEC có: góc BEC + góc ECB +góc CBE = 180o ( đ/lí tổng 3 góc )
=> góc CBE = 180o - góc BEC - góc ECB
=>góc CBE = 180o - 60o - 30o = 90o
Có: Góc ECB < góc BEC < góc CBE (vì 30o < 60o < 90o)
=> EB < BC < EC (quan hệ giữa góc và cạnh đối diện trong tam giác)

a.
EAB + BAC = 1800
EAB + 1200 = 1800
EAB = 1800 - 1200
EAB = 600
AD là tia phân giác của BAC
=> BAD = DAC = BAC/2 = 1200/2 = 600
AD // EB
=> DAB = EBA (2 góc so le trong)
mà DAB = EAB ( = 600 )
=> EBA = EAB
=> Tam giác EAB cân tại E
mà EAB = 600
=> Tam giác ABE đều
b.
BAC = 1200
=> Tam giác ABC tù
=> BC là cạnh lớn nhất
=> BC < AB
mà AB = EB (tam giác ABE đều)
=> BC < EB (1)
Tam giác ABC có:
BC < AB + AC (bất đẳng thức tam giác)
mà AB = AE (tam giác ABE đều)
=> BC < AB + AE
=> BC < EC (2)
Từ (1) và (2), ta có:
EC > BC > EB

vi be song song voi ad
ma ad vuong goc voi bc ( cho nay minh lam hoi tat)
vay vay be vuong goc voi bc ma goc EBA+ ABD = EBD = 90O
VAY EBA = 600
VAy eba =eab=600(cho nay ban phai tinh goc eab bang tc 2 goc ke bu)
vây tam gia abe deu
b(co 3 goc moi goc bang 90;60;30do ban tu giai dua vao tc canh doi dien voi goc lon hon)
t i c k nha

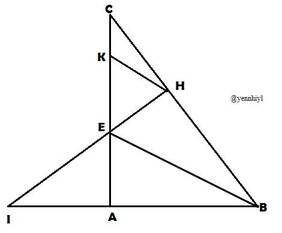
a) Xét \(\Delta ABE\) và \(\Delta HBE\):
BE chung
\(\widehat{ABE}=\widehat{EBH}\)
\(\widehat{EAB}=\widehat{EHB}=90^o\)
\(\Rightarrow\Delta ABE=\Delta HBE\left(ch-gn\right)\)
b) \(\widehat{EBH}=\dfrac{1}{2}\widehat{B}=30^o\)
\(\widehat{ACB}=90^o-\widehat{B}=30^o\)
\(\Rightarrow\Delta EBC\) cân tại E
Mà EH vuông góc BC
\(\Rightarrow HB=HC\)
c) \(\widehat{HEB}=90^o-\widehat{EBH}=60^o\)
\(KH//BE\Rightarrow\widehat{KHE}=\widehat{HEB}=60^o\)
\(\widehat{HEB}+\widehat{AEB}=60^o+60^o=120^o\)
\(\Rightarrow\widehat{KEH}=180^o-120^o=60^o\)
\(\Rightarrow\Delta EHK\) đều
d) Theo phần a. \(\Delta ABE=\Delta HBE\Rightarrow AE=EH\)
\(\Delta IAE\) vuông ở A \(\Rightarrow IE>AE\)
\(\Rightarrow IE>EH\)
a) Xét ΔABEΔABE và ΔHBEΔHBE:
BE chung
ˆABE=ˆEBHABE^=EBH^
ˆEAB=ˆEHB=90oEAB^=EHB^=90o
⇒ΔABE=ΔHBE(ch−gn)⇒ΔABE=ΔHBE(ch−gn)
b) ˆEBH=12ˆB=30oEBH^=12B^=30o
ˆACB=90o−ˆB=30oACB^=90o−B^=30o
⇒ΔEBC⇒ΔEBC cân tại E
Mà EH vuông góc BC
⇒HB=HC⇒HB=HC
c) ˆHEB=90o−ˆEBH=60oHEB^=90o−EBH^=60o
KH//BE⇒ˆKHE=ˆHEB=60oKH//BE⇒KHE^=HEB^=60o
ˆHEB+ˆAEB=60o+60o=120oHEB^+AEB^=60o+60o=120o
⇒ˆKEH=180o−120o=60o⇒KEH^=180o−120o=60o
⇒ΔEHK⇒ΔEHK đều
d) Theo phần a. ΔABE=ΔHBE⇒AE=EHΔABE=ΔHBE⇒AE=EH
ΔIAEΔIAE vuông ở A ⇒IE>AE