Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

minh bt đáp án là 26 nhưng k bt cách làm. 15 sai nhé bạn

Tam giác ABC có 2 đường trung tuyến vuông góc với nhau nên:
\(AB^2+AC^2=5BC^2\)
\(19^2+22^2=5BC^2\)
\(845=5BC^2\)
\(BC^2=169\)
\(BC=13\)
Vậy: Đoạn BC dài 13cm

Gọi giao điểm của BN, CM là G => G là trọng tâm của tam giác ABC
Ta có: BN vuông góc vs CM
=> BG vuông góc vs GM và CG vuông góc vs GN
=> MG2 + GB2 = BM2 =(1/2.AB)2 =90,25 và CG2 + GN2 = NC2 = (1/2AC)2 = 121 (ĐL Pytago)
=> MG2 + GB2 + CG2 + GN2 = 211,25
Mà MG = 1/2 CG và NG = 1/2 BG (Vì G là trọng tâm)
=> (1/2CG)2 + CG2 + (1/2 BG)2 + BG2 =211,25 => 5/4 BG2 + 5/4 CG2 =211,25
=> BG2 +CG2 = 211,25 : 5/4 =169
=> BC2 = 169 (Vì BG2 +CG2 = BC2) => BC = 13

gọi O là giao điểm của BN và CM.
theo đề bài, ta có:
AM=BM=19:2=9,5 cm
AN=NC=22:2=11 cm
MN là đường trung bình của tam giác ABC vì AM=MB; AN=NC
\(\Rightarrow\)BC=2MN
áp dụng ĐL pytago vào tam giác BOM, ta được:
\(BM^2=BO^2+OM^2=9,5^2=90,25cm\)(1)
áp dụng ĐL pytago vào tam giác OMN, ta được:
\(MN^2=MO^2+ON^2\)(2)
áp dụng ĐL pytago vào tam giác ONC, ta được:
\(CN^2=OC^2+ON^2=11^2=121cm\)(3)
áp dụng ĐL pytago vào tam giác BOC, ta được:
\(BC^2=BO^2+OC^2\)(4)
cộng vế theo vế phương trình
(1) và (3), ta được: \(BO^2+OM^2+ON^2+OC^2=211,25cm\)
hay \(BC^2+MN^2=211,25\)
hay \(BC^2+\left(\dfrac{BC}{2}\right)^2=211,25\)
\(\Leftrightarrow\dfrac{5BC^2}{4}=211,25cm\\ \Rightarrow BC=13cm\)
vậy BC=13 cm
Cho tam giác ABC vuông tại A. Các đường trung tuyến AM và BN vuông góc với nhau tại G, AB=a.tính BC?


Gọi G là giao điểm của BD và CE. Ta có G là trọng tâm của △ABC
Đặt GD=x,GE=y. Khi đó GB=2x,GC=2y.
Áp dụng định lý Pitago cho các tam giác vuông BGE, CGD, ta có:
GE2+GB2=BE2⇒y2+4x2=9 (1)
GD2+GC2=CD2⇒x2+4y2=16 (2)
Từ (1) và (2) ta có: 5(x2+y2)=25
⇒x2+y2=5
Áp dụng định lý Pitago cho tam giác vuông BGC, ta có:
BC2=GB2+GC2=4x2+4y2=20
Vậy: BC = \(\sqrt[2]{5}\)

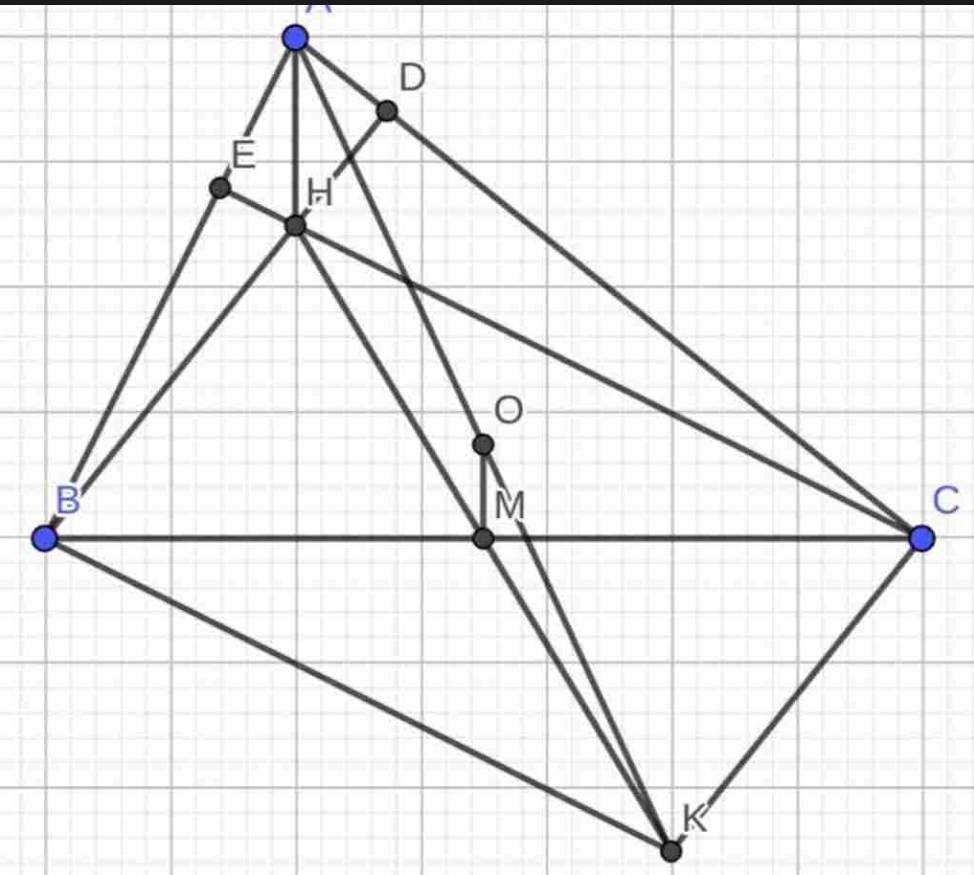
c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC