Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

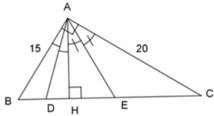
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 = > H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AD là phân giác của tam giác ABH nên: A B A H = B D D H ⇔ A B A H = B H − D H D H
⇔ 15 12 = 9 − D H D H ó 15DH = 108 – 12DH ó DH = 4cm
Đáp án: A

Bài 1:
Xét ΔABC có AD là phân giác
nen AB/BD=AC/CD
=>AB/3=AC/4
Đặt AB/3=AC/4=k
=>AB=3k; AC=4k
Ta có: \(AB^2+AC^2=BC^2\)
\(\Leftrightarrow25k^2=35^2\)
=>k2=49
=>k=7
=>AB=21cm; AC=28cm

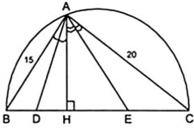
Áp dụng định lý Py – ta – go vào tam giác ABC vuông tại A, ta được:
B C 2 = A C + A B 2 ⇒ B C 2 = 15 2 + 20 2 ⇔ B C 2 = 25 2 ⇔ BC = 25( cm )
Đặt BD = x ⇒ DC = 25 - x
Áp dụng định lý Py 0 ta – go vào hai tam giác vuông AHB và AHC, ta được:
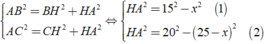
Trừ theo vế các đẳng thức ( 1 ) và ( 2 ) ta được:
15 2 - x 2 - 20 2 + ( 25 - x ) 2 = 0 ⇔ 50x = 450 ⇔ x = 9( cm )
Nên HC = 25 - 9 = 16( cm )
Thay x = 9 vào đẳng thức ( 1 ) ta có: H A 2 = 15 2 - 9 2 = 122 ⇔ HA = 12( cm )
Áp dụng tính chất đường phân giác AD vào tam giác AHB, ta được:
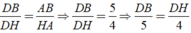
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
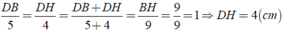
Áp dụng tính chất đường chất đường phân giác AE của tam giác ACH, ta được:
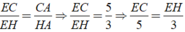
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
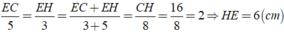

Ta có BC^2 = AB^2 + AC^2 = 625 => BC =25
=> AH = AB.AC/BC = 20.15/25 = 12
Do tính chất phân giác, ta có:
HD/DB = AH/AB= 12/15=4/5
=> HD/DB =4/5
=> DB/HD =5/4 => HB/HD =9/4 => HD =4HB/9
Mà HB^2 = AB^2 - AH^2 = 15^2 - 12^2 =81
=> HB=9 => HD = 4 ( cm )
Tương tự ta cũng có:
Do tính chất phân giác, ta có:
HE/EC = AH/AC= 12/20=3/5
=> HE/EC =3/5
=> EC/HE =5/3 => HC/HE =8/3 => HE =3HC/8
Mà HC^2 = AC^2 - AH^2 = 20^2 - 12^2 =256
=> HC=16 => HE = 6 ( cm )
Vậy HD = 4 ( cm ) và HE = 6 ( cm )
Ta có BC^2 = AB^2 + AC^2 = 625 => BC =25
=> AH = AB.AC/BC = 20.15/25 = 12
Do tính chất phân giác, ta có:
HD/DB = AH/AB= 12/15=4/5
=> HD/DB =4/5
=> DB/HD =5/4 => HB/HD =9/4 => HD =4HB/9
Mà HB^2 = AB^2 - AH^2 = 15^2 - 12^2 =81
=> HB=9 => HD = 4
====================
Tương tự
Do tính chất phân giác, ta có:
HE/EC = AH/AC= 12/20=3/5
=> HE/EC =3/5
=> EC/HE =5/3 => HC/HE =8/3 => HE =3HC/8
Mà HC^2 = AC^2 - AH^2 = 20^2 - 12^2 =256
=> HC=16 => HE = 6
Áp dụng định lý Pytago vào tam giác ABC vuông tại A, ta có:
A B 2 + A C 2 = B C 2 ⇔ 15 2 + 20 2 = B C 2 ⇒ B C = 25
Ta có: S A B C = 1 2 .AB.AC = 1 2 .AH.BC ⇒ A H = A B . A C B C = 15.20 25 = 12
Áp dụng định lý Pytago trong tam giác AHB vuông tại H, ta có:
A B 2 = A H 2 + H B 2 ⇔ 15 2 = 12 2 + H B 2 ⇒ H B 2 = 81 ⇒ H B = 9 ⇒ H C = B C – H B = 25 – 9 = 16
Vì AE là phân giác của tam giác CAH nên: A C A H = C E E H ⇔ A C A H = C H − H E E H
ó 20 12 = − H E H E ó 20HE = 12(16 – HE) ó 20HE + 12HE = 12.16
ó 32HE = 192 ó HE = 6(cm)
Đáp án: B