Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn D.
Ta có:
sin 2 α + cos 2 α = 1
sinα + 2cosα = -1 ⇔ sinα = -1 - 2cosα
⇔ (-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5 cos 2 α + 4cosα = 0
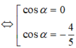
Vì π/2 < α < π ⇒ cosα < 0. Do đó, cos α = -4/5
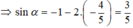
Ta lại có:
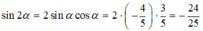
Ta có:
(sin α+cos α)^2
=sin^2α + 2sin α cos α + cos^2 α
=1+2sin α cos α
Nên A đúng
(sin α−cos α)^2
=sin^2 α−2sin α cos α+cos^2α
=(sin^2α+cos^2α)−2sin α cos α
=1−2sin α cos α
Nên B đúng
cos^4 α−sin^4 α
=(cos^2 α−sin^2 α)(cos^2 α+sin^2 α)
=(cos^2 α−sin^2 α).1
=cos^2 α−sin^2 α
Nên C đúng
cos^4 α+sin^4 α
=(sin^2 α+cos^2 α )^2−2sin^2 α cos^2 α
=1−2 sin^2 α cos^2 α.
Nên D sai chọn D
ko bít có đúng ko nx
Bạn ơi! Toán từ lớp 10 trở lên bạn vào hoc 24 để gửi câu hỏi nhé!
Bài này câu D sai.
Bạn thay \(\alpha=\frac{\pi}{2}\) vào thử nhé!
Chọn D.
Vì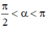 
⇒ sinα > 0, cosα < 0.
Từ sinα + 2cosα = -1 ⇒ sinα = -1 - 2cosα.
Ta có:
(-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5cos2α + 4cosα = 0
⇔ cosα.(5cosα + 4) = 0
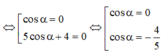
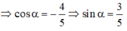
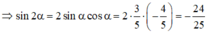
yvghtoyhlu4lworiorioriorioritfzgh dfkj gbvkjfdsj
vnfsmvgbjj cdtndgfbjfdhj gfhb gfkj
dgfhjsgs j fjb rtsfb hn
1732
4983268893574945866346785785784685467847858678675
c o t 2 α = 1 / ( sin 2 α ) – 1 = 25 / 20 – 1 = 1/4 ⇒ cotα = ±1/2.
Vì 3π/2 < α < 2π nên cotα < 0. Vậy cotα = (-1)/2.
Đáp án: C
Em tham khảo ở đây:
Cho a,b,c > 0 và ab + bc + ac = 1. Chứng minh rằng :\(\dfrac{a}{\sqrt{a^2+1}}+\dfrac{b}{\sqrt{b^2+1}}+\dfrac{c}{\sqrt{c^... - Hoc24
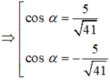
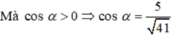
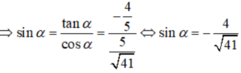
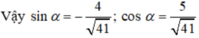
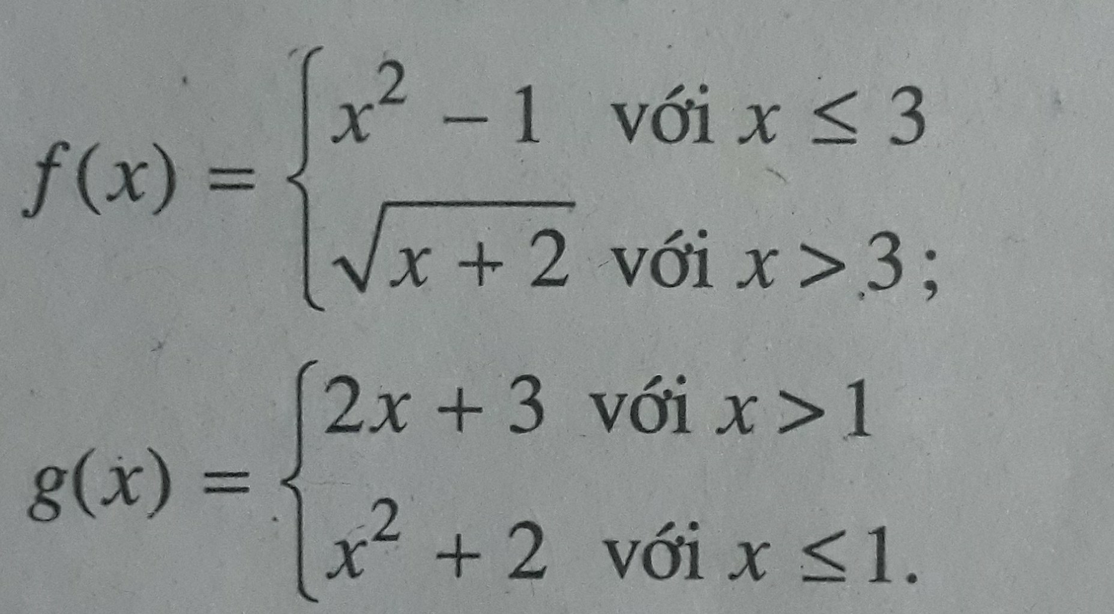
Chọn D.
Ta có: sin2α = a ⇒ 2sinα.cosα = a với 0 < α < 90o.
sin 2 α + cos 2 α = 1
⇔ sin 2 α + cos 2 α + 2sinαcosα - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 = 1 + 2sinαcosα
⇔ (sinα + cosα ) 2 = 1 + a