Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Ta có:
sin 2 α + cos 2 α = 1
sinα + 2cosα = -1 ⇔ sinα = -1 - 2cosα
⇔ (-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5 cos 2 α + 4cosα = 0
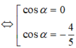
Vì π/2 < α < π ⇒ cosα < 0. Do đó, cos α = -4/5
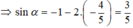
Ta lại có:
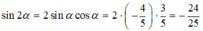

Chọn D.
Ta có: sin2α = a ⇒ 2sinα.cosα = a với 0 < α < 90o.
sin 2 α + cos 2 α = 1
⇔ sin 2 α + cos 2 α + 2sinαcosα - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 - 2sinαcosα = 1
⇔ (sinα + cosα ) 2 = 1 + 2sinαcosα
⇔ (sinα + cosα ) 2 = 1 + a


Chọn C.
Áp dụng công thức: cos2α = 1 - 2 sin 2 α = 1 - 2.(0,6 ) 2 = 0,28

3/4pi<a<pi
=>sin a>0; cosa<0
sin2a=-4/5
=>2*sina*cosa=-4/5
=>sina*cosa=-2/5
(sina-cosa)^2=sin^2a+cos^2a-2*sina*cosa=1+4/5=9/5
=>sin a-cosa=3/căn 5
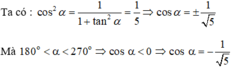
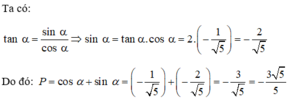
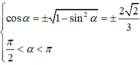
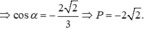
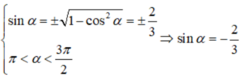
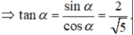
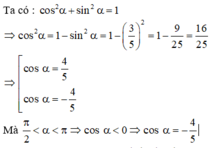
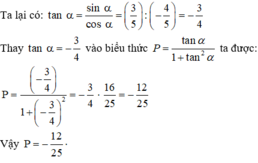
Chọn D.
Vì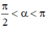 ⇒ sinα > 0, cosα < 0.
⇒ sinα > 0, cosα < 0.
Từ sinα + 2cosα = -1 ⇒ sinα = -1 - 2cosα.
Ta có:
(-1 - 2cosα ) 2 + cos 2 α = 1
⇔ 1 + 4cosα + 4 cos 2 α + cos 2 α = 1
⇔ 5cos2α + 4cosα = 0
⇔ cosα.(5cosα + 4) = 0