Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)xét ΔADC và ΔABC có:
AC là cạnh chung
\(\widehat{DAC}=\widehat{BCA}\)(2 góc sole trong)
\(\widehat{DCA}=\widehat{BAC}\)(2 góc sole trong)
⇒ΔADC=ΔABC(g-c-g)
⇒AD=BC(2 cạnh tương ứng)
AB=DC(2 cạnh tương ứng)
b)xét ΔAOD và ΔBOC có:
\(\widehat{ADO}=\widehat{CBO}\)(2 góc sole trong)
\(\widehat{BCO}=\widehat{DAO}\)(2 góc sole trong)
AD=BC(câu a)
⇒ΔAOD=ΔBOC(g-c-g)
⇒AO=CO(2 cạnh tương ứng)
⇒O là trung điểm của AC
vì ΔAOD=ΔBOC ⇒DO=BO(2 cạnh tương ứng)
⇒O là trung điểm của BD
hay O cùng là trung điểm của AC và BD(đ.p.ch/m)
c)xét ΔAOM và ΔCOP có:
AC=CO(O là trung điểm của AC)
\(\widehat{AOM}=\widehat{COP}\)(2 góc đối đỉnh)
\(\widehat{MAO}=\widehat{BCO}\)(2 góc sole trong)
⇒ΔAOM=ΔCOP(g-c-g)
⇒MO=PO(2 cạnh tương ứng)
⇒O là trung điểm của MP(đ.p.ch/m)

Vì AD//BC => góc DAC= góc ACB (so le trong)(1)
AB//CD => góc BAC=góc ACD (so le trong) (2)
Mà Δ ABC và Δ ACD có cạnh AC chung (3)
Từ (1),(2),(3) => Δ ACB=Δ CAD ( g.c.g)
=> AD=BC và AB=CD

a) Do AD // BC (gt) => góc DAC = góc ACB (so le trong)
AB // CD (gt) => góc BAC = góc ACD (so le trong)
Xét t/giác ABC và t/giác CDA
có góc ACB = góc DAC (cmt)
AC : chung
góc BAC = góc ACD (cmt)
=> t/giác ABC = t/giác CDA (g.c.g)
b) Ta có : t/giác ABC = t/giác CDA (cmt)
=> AB = CD (hai cạnh tương ứng)
Do AB // CD (gt) => góc ABD = góc BDC (so le trong)
Xét t/giác AMB và t/giác CMD
có góc BAM = góc MCD (cmt)
AB = CD (cmt)
góc ABM = góc BDM (cmt)
=> t/giác AMB = t/giác CMD (g.c.g)
=> AM = MC (hai cạnh tương ứng)
=> M là trung điểm của AC
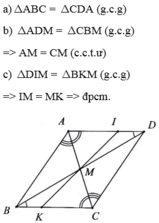
c) Xét t/giác AMI và t/giác CMK
có góc DAC = góc ACK (cmt)
AM = CM (cmt)
góc IMA = góc CMK (đối đỉnh)
=> t/giác AMI = t/giác CMK (g.c.g)
=> MI = MK (hai cạnh tương ứng)
=> M là trung điểm của IK
Kuroba Kaito, mình đã biết I, M, K có thẳng hàng đâu. mới chứng minh được MI=Mk nên chưa thể nói M là trung điểm của IK được