Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC và ΔCDA có
\(\widehat{ACB}=\widehat{CAD}\)
AC chung
\(\widehat{CAB}=\widehat{ACD}\)
Do đó: ΔABC=ΔCDA
b: Xét tứ giác ABCD có
AB//CD
AD//BC
Do đó: ABCD là hình bình hành
Suy ra: Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường
hay M là trung điểm của AC
c: Xét ΔAMI và ΔCMK có
\(\widehat{IAM}=\widehat{KCM}\)
AM=CM
\(\widehat{AMI}=\widehat{CMK}\)
Do đó: ΔAMI=ΔCMK
Suy ra: MI=MK
mà M,I,K thẳng hàng
nên M là trung điểm của IK

\(\text{a)Ta có:AD//BC}\Rightarrow\widehat{CAD}=\widehat{ACB}\text{(so le trong)}\)
\(\text{AB//CD}\Rightarrow\widehat{BAC}=\widehat{ACD}\text{(so le trong)}\)
\(\text{Xét }\Delta ABC\text{ và }\Delta CAD\text{ có:}\)
\(\widehat{CAD}=\widehat{ACB}\text{(so le trong)}\)
\(\widehat{BAC}=\widehat{ACD}\text{(so le trong)}\)
\(AC\text{ chung}\)
\(\Rightarrow\Delta ABC=\Delta CAD\left(c.g.c\right)\)
\(\Rightarrow\text{BC=AD(hai cạnh tương ứng)}\)
\(\text{b)}\text{Xét }\Delta AMD\text{ và }\Delta BMC\text{ có:}\)
\(\widehat{BCM}=\widehat{CAD}\text{(đối đỉnh)}\)
\(\widehat{BMC}=\widehat{AMD}\text{(đối đỉnh)}\)
\(\Rightarrow\widehat{CBM}=\widehat{AMD}\)
\(\text{Xét }\Delta AMD\text{ và }\Delta BMC\text{ có:}\)
\(\widehat{BMC}=\widehat{CAD}\text{(so le trong)}\)
\(\text{ BC=AD (cmt)}\)
\(\widehat{CBM}=\widehat{AMD}\left(cmt\right)\)
\(\Rightarrow\Delta AMD=\Delta BMC\left(g.c.g\right)\)
\(\Rightarrow\text{AM=CM(2 cạnh tương ứng)}\)
\(\Rightarrow\text{M là trung điểm của AC}\)
\(\text{c)Xét }\Delta AMI\text{ và }\Delta CMK\text{ có:}\)
\(\widehat{BCM}=\widehat{CAD}\text{(so le trong)}\)
\(\text{AM=CM (cmt)}\)
\(\widehat{CMK}=\widehat{AMI}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta AMI=\Delta CMK\left(g.c.g\right)\)
\(\Rightarrow\text{MI=MK}\)
\(\Rightarrow\text{M là trung điểm của IK}\)

BD cắt AC tại O.
-△ABC=△CDA (g-c-g) \(\Rightarrow AB=DC\)
\(\Rightarrow\)△ABO=△CDO (g-c-g) \(\Rightarrow OA=OC\Rightarrow\)O là trung điểm AC.
-△ABC có: Trung tuyến BO cắt trung tuyến CE tại M.
\(\Rightarrow\)M là trọng tâm của △ABC mà F là trung điểm BC.
\(\Rightarrow\)A,M,F thẳng hàng.

a: Xét tứ giác ABCD có
AD//BC
AB//CD
Do đó: ABCD là hình bình hành
Suy ra: BC=AD
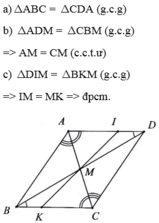
a) Do AD // BC (gt) => góc DAC = góc ACB (so le trong)
AB // CD (gt) => góc BAC = góc ACD (so le trong)
Xét t/giác ABC và t/giác CDA
có góc ACB = góc DAC (cmt)
AC : chung
góc BAC = góc ACD (cmt)
=> t/giác ABC = t/giác CDA (g.c.g)
b) Ta có : t/giác ABC = t/giác CDA (cmt)
=> AB = CD (hai cạnh tương ứng)
Do AB // CD (gt) => góc ABD = góc BDC (so le trong)
Xét t/giác AMB và t/giác CMD
có góc BAM = góc MCD (cmt)
AB = CD (cmt)
góc ABM = góc BDM (cmt)
=> t/giác AMB = t/giác CMD (g.c.g)
=> AM = MC (hai cạnh tương ứng)
=> M là trung điểm của AC
c) Xét t/giác AMI và t/giác CMK
có góc DAC = góc ACK (cmt)
AM = CM (cmt)
góc IMA = góc CMK (đối đỉnh)
=> t/giác AMI = t/giác CMK (g.c.g)
=> MI = MK (hai cạnh tương ứng)
=> M là trung điểm của IK
Kuroba Kaito, mình đã biết I, M, K có thẳng hàng đâu. mới chứng minh được MI=Mk nên chưa thể nói M là trung điểm của IK được