Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ờm hình bạn tự vẽ nha, à mà mình chỉ làm tới câu b thôi
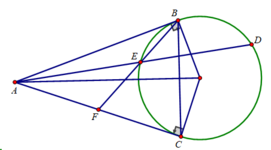
a, Gọi giao điểm của AC và BF là M, giao điểm của AD và BE là G
(O;R) có: \(\widehat{ABC}=\widehat{ABD}=90^o\)(góc nội tiếp chắn nửa đường tròn)
Ta có: \(\widehat{ABC}+\widehat{ABD}=\widehat{CBD}\)
hay \(90^o+90^o=\widehat{CBD}\)\(\Rightarrow\widehat{CBD}=180^o\)nên C,B,D thẳng hàng
Ta có: \(\widehat{AEB}=\widehat{AFB}\)(cùng chắn \(\stackrel\frown{AB}\)) (1)
(O;R) có: \(AD\perp BE,AD\cap BE=\left\{G\right\},AD=2R\)\(\Rightarrow BG=GE\)(liên hệ giữa cung và dây)
\(\Delta ABE\) có AG vừa là trung tuyến, vừa là đường cao nên \(\Delta ABE\)cân tại A nên \(\widehat{ABE}=\widehat{AEB}\)(2)
Chứng minh tương tự ta được \(\Delta AFB\)cân tại A nên \(\widehat{AFB}=\widehat{ABF}\)(3)
Từ (1), (2), (3) ta được \(\widehat{ABE}=\widehat{ABF}\)nên BA là phân giác của \(\widehat{EBF}\)
b, (O;R) có: \(\widehat{FAC}=\dfrac{1}{2}\stackrel\frown{FC},\widehat{KCF}=\dfrac{1}{2}\stackrel\frown{FC}\)(góc nội tiếp = 1/2 cung) \(\Rightarrow\widehat{KCF}=\widehat{FAC}\)
Xét \(\Delta KHC\) và \(\Delta CFA\) có:
\(HC=AF\left(gt\right)\)
\(\widehat{KHC}=\widehat{CFA}=90^o\)
\(\widehat{HCK}=\widehat{FAC}\left(cmt\right)\)
\(\Rightarrow\Delta KHC=\Delta CFA\left(g-c-g\right)\Rightarrow HK=FC\)
Ta có: \(\widehat{ABE}+\widehat{EBD}=90^o\)mà \(\widehat{ABE}=\widehat{ABF}\)nên \(\widehat{EBD}+\widehat{ABF}=90^o\)mà \(\widehat{AFB}=\widehat{ABF}\)nên \(\widehat{EBD}+\widehat{AFB}=90^o\)
\(\Delta MFA\) có: \(\widehat{FMA}=90^o\)\(\Rightarrow\widehat{MFA}+\widehat{MAF}=90^o\)
Từ 2 điều trên ta được \(\widehat{EBD}=\widehat{MAF}\)mà \(\widehat{KCF}=\widehat{CAF}\)nên \(\widehat{KCF}=\widehat{EBD}\)

1. Ta có:\(\widehat{DAB}\)=\(\dfrac{1}{2}\)sđ cung DB
\(\widehat{BDE}\)=\(\dfrac{1}{2}\)sđ cung DB
\(\Rightarrow\)\(\widehat{DAB}\)=\(\widehat{BDE}\)
3. cmtt câu a ta có: \(\widehat{DEB}\)=\(\widehat{BAE}\)
Ta có: \(\widehat{EDB}\)+\(\widehat{DEB}\)+\(\widehat{DBE}\)=180
=> \(\widehat{BAE}\)+\(\widehat{BAD}\)+\(\widehat{PBQ}\)=180
Vì \(\widehat{PBQ}\)=\(\widehat{DBE}\) ( đối đỉnh)
=> \(\widehat{DAE}\)+\(\widehat{PBQ}\)=180
=> PBQA nội tiếp => \(\widehat{DAB}\)=\(\widehat{BQP}\)
Mà \(\widehat{DAB}\)=\(\widehat{BDE}\)=> \(\widehat{BQP}\)=\(\widehat{BDE}\)
=> PQ// DE