Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

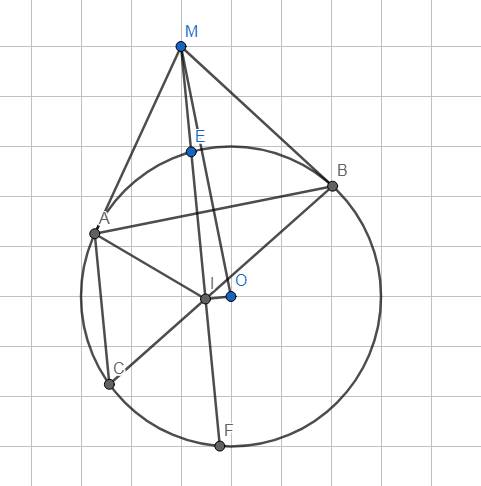
Từ một điểm M ở bên ngoài đường tròn tâm O, vẽ hai tiếp tuyến MA, MB với đường tròn (O)( A, B là các tiếp điểm). Gọi E là trung điểm của đoạn thẳng MA, tia EB cắt đường tròn (O) tại C. Tia MC cắt đường tròn (O) tại điểm thứ hai là D. Chứng minh rằng:
a. Tứ giác MAOB nội tiếp;
b. EA2 = EC.EB;
c. BD // MA.

Bạn tự vẽ hình nha
a)Xét tứ giác MAOB có:
\(\widehat{MAO}\)=90'(vì MA là tiếp tuyến của (O))
\(\widehat{MBO}\)=90'(vì MB là tiếp tuyến của (O))
Suy ra \(\widehat{MAO}\)+\(\widehat{MBO}\)=90'+90'=180'
Vậy tứ giác MAOB nội tiếp
b)Xét tam giác ABM có:
MA=MB(tính chất hai tiếp tuyến cắt nhau)
Do đó tam giác MAB là tam giác cân tại M
c)Xét tam giác IBF và IAB có:
\(\widehat{BIA}\)là góc chung
\(\widehat{IBF}\)=\(\widehat{IAB}\)(cùng bằng 1/2 sđ\(\widebat{BF}\))
Do đó tam giác IBF đồng dạng với IAB
Suy ra \(\frac{IB}{IF}=\frac{IA}{IB}\)
<=>\(IB^2=IA.IF\)

*Mấu chốt bài này là c/m 5 điểm M,A,I,O,B nằm trên cùng 1 đg tròn.
- Ta có: △OAM vuông tại A, △OBM vuông tại B.
\(\Rightarrow\)△OAM, △OBM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)AMBO nội tiếp đường tròn đường kính OM (1).
- Ta có AC//EF \(\Rightarrow\widehat{ACB}=\widehat{MIB}\) (2 góc so le trong).
- Trong (O) có:
\(\widehat{ACB}\) là góc nội tiếp chắn cung AB.
\(\widehat{MAB}\) là góc tạo bởi tia tiếp tuyến MA và dây cung AB.
\(\Rightarrow\widehat{ACB}=\widehat{MAB}\)
\(\Rightarrow\widehat{MAB}=\widehat{MIB}\). Do đó AIBM nội tiếp (2). (2 góc cùng nhìn 1 cạnh bằng nhau).
\(\left(1\right),\left(2\right)\Rightarrow\)A,M,B,O,I cùng nằm trên đường tròn đường kính OM.
\(\Rightarrow\)△OIM nội tiếp đường tròn đường kính OM.
\(\Rightarrow\)△OIM vuông tại I nên OI vuông góc với EF tại I.
Trong (O): EF là dây cung, OI là 1 phần đường kính, \(OI\perp EF\) tại I..
\(\Rightarrow\)I là trung điểm EF (đpcm).


( mấy cái cơ bản thì tự viết nhé )
a) góc MAO và góc MBO= 90 độ
xét tứ giác MAOB có góc MAO+MBO=180 độ
=> MAOB nội tiếp
b) Xét (O) có EB là tiếp tuyến của (O)
\(\Rightarrow\widehat{EBD}=\widehat{EAB}\left(=\frac{1}{2}sđ\widebat{DB}\right)\)
Xét tam giác EDB và tam giác EBA có:
\(\hept{\begin{cases}\widehat{AEB}chung\\\widehat{EBD}=\widehat{EAB}\left(cmt\right)\end{cases}\Rightarrow\Delta EDB~\Delta EBA\left(g-g\right)}\)
\(\Rightarrow\frac{BE}{DE}=\frac{AE}{BE}\)
\(\Rightarrow BE^2=AE.DE\left(1\right)\)
Vì \(AC//MB\Rightarrow\widehat{ACM}=\widehat{DME}\left(SLT\right)\)
Ta có: \(\hept{\begin{cases}\widehat{ACM}=\widehat{ABD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\\\widehat{ABD}=\widehat{MAD}\left(=\frac{1}{2}sđo\widebat{AD}\right)\end{cases}\Rightarrow\widehat{ACM}=\widehat{MAD}}\)
\(\Rightarrow\widehat{DME}=\widehat{MAD}\)
Xét tam giác EMD và tam giác EAM có:
\(\hept{\begin{cases}\widehat{DME}=\widehat{MAD}\\\widehat{AME}chung\end{cases}}\Rightarrow\Delta EMD~\Delta EAM\left(g-g\right)\)
\(\Rightarrow\frac{ME}{DE}=\frac{AE}{ME}\)
\(\Rightarrow ME^2=DE.AE\left(2\right)\)
Từ (1) và (2) \(\Rightarrow BE=ME\left(đpcm\right)\)
c) mai nốt :V
c) El à trung điểm MB;H là trung điểm AB
-> EH là đường trung bình tam giác MAB
=> EH// MA
=> góc EHB= góc MAB ( đồng vị )
Mà góc MAB = góc AKB ( = 1/2 số đo cung AB )
=> góc EHB= góc AKB
mà góc EHB+ góc IHB = 180 độ
=> góc AKB + góc IHB = 180 độ
=> BHIK nội tiếp
=> góc BHK= BIK mà góc BHK= 90 độ
=> góc BIK= 90 độ
=> AK vuông góc với BI