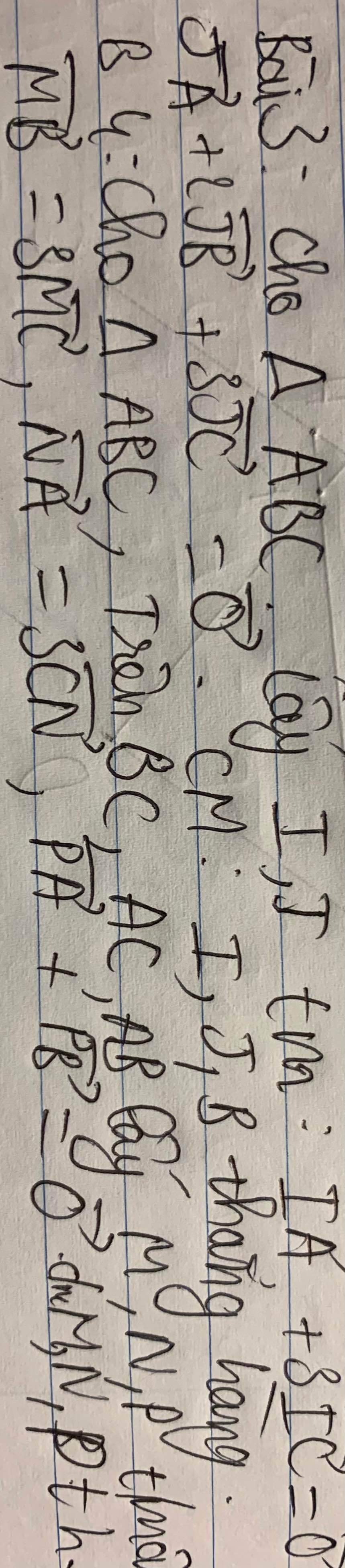KT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
8 tháng 3 2022
\(mx^2+\left(m-1\right)x+3-4m=0\left(1\right)\)
\(m=0\Rightarrow\)\(\left(1\right)\Leftrightarrow-x+3=0\Leftrightarrow x=3\left(ktm\right)\)
\(m\ne0\Rightarrow x1< 2< x2\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\\left(x1-2\right)\left(x2-2\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)^2-4m\left(3-4m\right)>0\\x1x2-2\left(x1+x2\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\\dfrac{3-4m}{m}-2.\left(\dfrac{1-m}{m}\right)+4< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m>\dfrac{7+4\sqrt{2}}{17}\\m< \dfrac{7-4\sqrt{2}}{17}\end{matrix}\right.\\-\dfrac{1}{2}< m< 0\\\end{matrix}\right.\)\(\Rightarrow m\in\phi\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2019
a/ \(n^2+12n+8=k^2\)
\(\Leftrightarrow\left(n+6\right)^2-28=k^2\)
\(\Leftrightarrow\left(n+6\right)^2-k^2=28\)
\(\Leftrightarrow\left(n-k+6\right)\left(n+k+6\right)=28\)
Do \(n-k+6+n+k+6=2n+12\) chẵn nên ta chỉ cần xét các cặp ước chẵn của 28
\(\Rightarrow\left(n-k+6\right)\left(n+k+6\right)=2.14\)
\(\Rightarrow\left\{{}\begin{matrix}n-k+6=2\\n+k+6=14\end{matrix}\right.\) \(\Rightarrow n=2\)
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 11 2019
b/ Do \(b\ge a\Rightarrow b^2+4a+3\le b^2+4b+3< b^2+4b+4=\left(b+2\right)^2\)
Mặt khác \(b^2+4a+3>b^2\)
\(\Rightarrow b^2< b^2+4a+3< \left(b+2\right)^2\)
\(\Rightarrow b^2+4a+3=\left(b+1\right)^2\)
\(\Leftrightarrow b=2a+1\)
\(\Rightarrow a^2-5b+30=a^2-5\left(2a+1\right)+30=a^2-10a+25=\left(a-5\right)^2\)
TT
14 tháng 8 2020
Đề bài : Chứng minh rằng tổng lập phương của các số tự nhiên liên tiếp từ 1 đến n bằng bình phương của tổng từ 1 đến n ( n tự nhiên ). Hay ta cần chứng minh : \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) (*)
Lời giải :
+) Xét \(n=1\) thì ta có : \(1^3=1^2\) ( đúng )
Suy ra (*) đúng với \(n=1\) (1)
+) Xét \(n=2\) ta có : \(1^3+2^3=1+8=9\); \(\left(1+2\right)^2=3^2=9\)
\(\Rightarrow1^3+2^3=\left(1+2\right)^2\) ( đúng ). Nên (*) đúng với \(n=2\) (2)
+) Giả sử (*) đúng với \(n=k\). Tức là : \(1^3+2^3+3^3+....+k^3=\left(1+2+...+k\right)^2\).
Ta cần chứng minh \(n=k+1\) cũng đúng với (*). Thật vậy , ta có :
\(1^3+2^3+3^3+.....+\left(k+1\right)^3\)
\(=1^3+2^3+....+k^3+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+\left(k+1\right)^3\)
Xét biểu thức \(\left(k+1\right)^2+2.\left(k+1\right).\left(1+2+3+....+k\right)\)
\(=\left(k+1\right)^2+2.\left(k+1\right)\cdot\frac{\left(k+1\right).k}{2}\)
\(=\left(k+1\right)^2+\left(k+1\right)^2.k=\left(k+1\right)^3\)
Do đó \(1^3+2^3+....+\left(k+1\right)^3\)
\(=\left(1+2+3+....+k\right)^2+2.\left(k+1\right)\left(1+2+....+k\right)+\left(k+1\right)^2\)
\(=\left(1+2+3+....+k+k+1\right)^2\)
Vậy (*) đúng với \(n=k+1\) (3)
Từ (1) (2) và (3) suy ra \(1^3+2^3+3^3+4^3+....+n^3=\left(1+2+....+n\right)^2\) với mọi \(n\in N\).
22 tháng 12 2021
a: Để phương trình có hai nghiệm trái dấu thì m+2<0
hay m<-2
NH
1
20 tháng 12 2022
vecto AI=1/2*vecto AM
=1/4(vecto AB+vecto AC)
=1/4(vecto AC+vecto CB+vecto AC)
=1/4(-2vecto CA+vecto CB)
=-1/2*vecto CA+1/4*vecto CB
=>m=-1/2; n=1/4
QD
2
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
3.
\(\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\Rightarrow\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{IB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{BC}=\overrightarrow{0}\Rightarrow4\overrightarrow{IB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (1)
\(\overrightarrow{JA}+2\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}+\overrightarrow{BA}+2\overrightarrow{JB}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow6\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{BC}=0\Rightarrow6\overrightarrow{JB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (2)
(1);(2) \(\Rightarrow4\overrightarrow{IB}=6\overrightarrow{JB}\Rightarrow\overrightarrow{IB}\) và \(\overrightarrow{JB}\) cùng phương
Hay I; J; B thẳng hàng
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 10 2021
4.
\(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\Rightarrow\overrightarrow{PA}+\overrightarrow{PA}+\overrightarrow{AB}=0\Rightarrow\overrightarrow{PA}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{NA}=3\overrightarrow{CN}\Rightarrow\overrightarrow{NA}=3\overrightarrow{CA}+3\overrightarrow{AN}\Rightarrow4\overrightarrow{AN}=3\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow2\overrightarrow{BM}=3\overrightarrow{BC}\Rightarrow\overrightarrow{BM}=\dfrac{3}{2}\overrightarrow{BC}=\dfrac{3}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) (1)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=-\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=2\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\) (2)
(1);(2) \(\Rightarrow\overrightarrow{PM}=2\overrightarrow{PN}\Rightarrow\) P, M, N thẳng hàng
