Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+3\ge\dfrac{2\left(a+b+c\right)}{abc}=2\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right)\)
Đặt \(\left(\dfrac{1}{a};\dfrac{1}{b};\dfrac{1}{c}\right)=\left(x;y;z\right)\Rightarrow xyz=1\)
BĐT trở thành: \(x^2+y^2+z^2+3\ge2\left(xy+yz+zx\right)\)
Theo nguyên lý Dirichlet, trong 3 số x;y;z luôn có ít nhất 2 số cùng phía so với 1
Không mất tính tổng quát, giả sử đó là x và y \(\Rightarrow\left(x-1\right)\left(y-1\right)\ge0\)
\(\Rightarrow xy+1\ge x+y\Rightarrow xyz+z\ge xz+yz\Rightarrow2xyz+2z\ge2xz+2yz\)
\(\Rightarrow2\ge2xz+2yz-2z\) (do \(xyz=1\))
\(\Rightarrow VP=x^2+y^2+z^2+2+1\ge x^2+y^2+z^2+2xz+2yz-2z+1\)
\(VP\ge2xy+z^2+2xz+2yz-2z+1=2\left(xy+yz+zx\right)+\left(z-1\right)^2\ge2\left(xy+yz+zx\right)\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=1\) hay \(a=b=c=1\)

\(a,\overrightarrow{AB}-\overrightarrow{DA}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{0}=\overrightarrow{AD}\)
\(b,\overrightarrow{AM}=\dfrac{\overrightarrow{AO}+\overrightarrow{AB}}{2}=\dfrac{\overrightarrow{AB}}{2}+\dfrac{\dfrac{1}{2}\overrightarrow{AC}}{2}=\overrightarrow{\dfrac{AB}{2}}+\dfrac{1}{4}\overrightarrow{AC}\)
\(=\overrightarrow{\dfrac{AB}{2}}+\dfrac{\overrightarrow{AB}+\overrightarrow{BC}}{4}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{\overrightarrow{BC}}{4}=\dfrac{1}{4}\overrightarrow{BC}+\dfrac{3}{4}\overrightarrow{AB}\left(1\right)\)
\(\overrightarrow{AN}=\overrightarrow{BN}-\overrightarrow{BA}=k.\overrightarrow{BC}+\overrightarrow{AB}\left(2\right)\)
\(\left(1\right)\left(2\right)A,M,N\) \(thẳng\) \(hàng\Leftrightarrow\dfrac{k}{\dfrac{1}{4}}=\dfrac{1}{\dfrac{3}{4}}\Leftrightarrow k=\dfrac{1}{3}\)
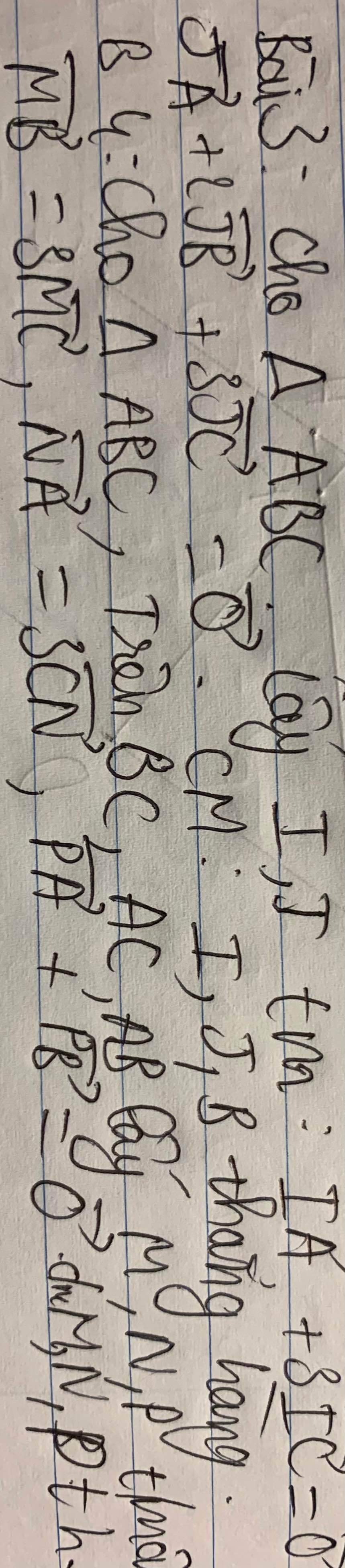
3.
\(\overrightarrow{IA}+3\overrightarrow{IC}=\overrightarrow{0}\Rightarrow\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{IB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow4\overrightarrow{IB}+\overrightarrow{BA}+3\overrightarrow{BC}=\overrightarrow{0}\Rightarrow4\overrightarrow{IB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (1)
\(\overrightarrow{JA}+2\overrightarrow{JB}+3\overrightarrow{JC}=\overrightarrow{0}\Rightarrow\overrightarrow{JB}+\overrightarrow{BA}+2\overrightarrow{JB}+3\overrightarrow{JB}+3\overrightarrow{BC}=\overrightarrow{0}\)
\(\Rightarrow6\overrightarrow{JB}+\overrightarrow{BA}+3\overrightarrow{BC}=0\Rightarrow6\overrightarrow{JB}=\overrightarrow{AB}+3\overrightarrow{CB}\) (2)
(1);(2) \(\Rightarrow4\overrightarrow{IB}=6\overrightarrow{JB}\Rightarrow\overrightarrow{IB}\) và \(\overrightarrow{JB}\) cùng phương
Hay I; J; B thẳng hàng
4.
\(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\Rightarrow\overrightarrow{PA}+\overrightarrow{PA}+\overrightarrow{AB}=0\Rightarrow\overrightarrow{PA}=-\dfrac{1}{2}\overrightarrow{AB}\)
\(\overrightarrow{NA}=3\overrightarrow{CN}\Rightarrow\overrightarrow{NA}=3\overrightarrow{CA}+3\overrightarrow{AN}\Rightarrow4\overrightarrow{AN}=3\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AN}=\dfrac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow2\overrightarrow{BM}=3\overrightarrow{BC}\Rightarrow\overrightarrow{BM}=\dfrac{3}{2}\overrightarrow{BC}=\dfrac{3}{2}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{PN}=\overrightarrow{PA}+\overrightarrow{AN}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\) (1)
\(\overrightarrow{PM}=\overrightarrow{PB}+\overrightarrow{BM}=\dfrac{1}{2}\overrightarrow{AB}-\dfrac{3}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=-\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}=2\left(-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)\) (2)
(1);(2) \(\Rightarrow\overrightarrow{PM}=2\overrightarrow{PN}\Rightarrow\) P, M, N thẳng hàng