J
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
18 tháng 10 2019
Đáp án C.
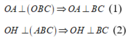
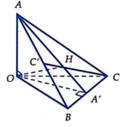
Từ (1) và (2) suy ra
=> AH là đường cao trong tam giác BCD
Tương tự suy ra, CH là đường cao trong tam giác BCD => H là trực tâm => I đúng => II sai
+ Gọi 
=> 1 O H 2 = 1 O B 2 + 1 O C 2 => 1 O H 2 = 1 O A ' 2 + 1 O A 2 = 1 O H 2 = 1 O A 2 + 1 O B 2 + 1 O C 2
=> III đúng
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 9 2021
Ta có: I là trung điểm SA, J là trung điểm SB \(\Rightarrow\) IJ là đường trung bình tam giác SAB
\(\Rightarrow IJ||AB\Rightarrow IJ||CD\)
\(\Rightarrow CD||\left(IJK\right)\)
CM
2 tháng 10 2018
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
c) Gọi X là biến cố :” có ít nhất một động cơ chạy tốt” thì X là biến cố đối của :
Chọn D
CM
1 tháng 3 2018
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
a) A1, A2, A3 là biến cố:” cả 3 biến cố đều chạy tốt ”
P(A1. A2. A3)= P(A1). P(A2). P(A3)= 0,504
Chọn C
CM
25 tháng 11 2017
Đáp án C
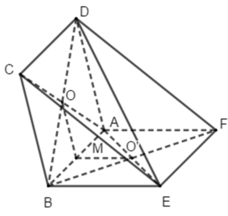
+) Ta có: BC // AD; BE // AF (ABCD và ABEF là hình bình hành)
Suy ra BC // (ADF); BE // (ADF)
Mà BC ∩ BE = B
Do đó (ADF) // (BEC).
+) O và O’ lần lượt là tâm của hình bình hành ABCD và ABEF nên O và O’ là trung điểm của BF và BD
Xét tam giác ABF có MO’ là đường trung bình nên MO’ // AF
MO’ // (ADF) (1)
Tương tự MO là đường trung bình của tam giác ABD nên MO // AD
MO // (ADF) (2)
Từ (1) và (2) suy ra (MOO’) // (ADF)
+) Chứng minh tương tự ta cũng có (MOO’) // (BCE).
+) Hai mặt phẳng (AEC) và (BDF) có:
AC ∩ DB = O ; AE ∩ BF = O’
Suy ra (AEC) ∩ (BDF) = OO’.
Vậy khẳng định (I); (II); (III) đúng.
CM
1 tháng 5 2017
+ Ta có IJ là đường trung bình của tam giác SAB nên IJ// AB// CD
=> IJCD là hình thang. Do đó A đúng.
+ Ta có I B ⊂ S A B I B ⊂ I B C ⇒ S A B ∩ I B C = I B . Do đó B đúng.
+ Ta có J D ⊂ S B D J D ⊂ J B D ⇒ S B D ∩ J B D = J D . Do đó C đúng.
+ Trong mặt phẳng (IJCD), gọi IC và JD cắt nhau tại M .,
=> giao tuyến của mặt phẳng (IAC) và (JBD) là MO
Do đó D sai.
Chọn D.
CM
9 tháng 11 2019
Gọi Ai là biến cố:” động cơ i chạy tốt” i=1,2,3
P(A1)= 0,7 ; P(A2).= 0,8 ; P(A3)=0,9 và A1, A2, A3 độc lập với nhau
Chọn A
