Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình làm cũng hoang mang lắm bạn=), hay để hỏi cô xem sao

a/ Ta có: AB vuông góc với BC, SC vuông góc với BC (vì SC vuông góc với mặt đáy ABCD). Vậy AB // SC. Vậy AB vuông góc (SBC).
b/ Tương tự, ta có: AD vuông góc với CD, SC vuông góc với CD. Vậy AD // SC. Vậy AD vuông góc (SCD).
c/ Ta có: SA vuông góc với mặt đáy ABCD (vì S là đỉnh chóp), CI vuông góc với SB (vì đường thẳng CI là hình chiếu của đường thẳng SC lên mặt phẳng chứa SB và CI). Vậy SA // CI. Vậy SA vuông góc CI.
d/ Gọi M là trung điểm của IJ. Ta cần chứng minh SA vuông góc CM. Ta có: CM vuông góc với IJ (vì nằm trên đường trung trực của IJ). Ta cũng có: SA vuông góc CI (đã chứng minh ở câu c). Vậy ta cần chứng minh CI // JM. Từ đó suy ra (SAC) ⊥ (CIJ). Theo tính chất của hình học không gian, ta có CI vuông góc với mặt phẳng (SBC). Tương tự, JI vuông góc với mặt phẳng (SCD). Vậy CI // JI. Điều này suy ra từ tính chất của mặt phẳng và đoạn thẳng vuông góc với mặt phẳng. Suốt đoạn thẳng IJ, ta có thể lấy một điểm nào đó làm trung điểm, ví dụ M. Vậy CI // JM.
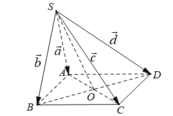
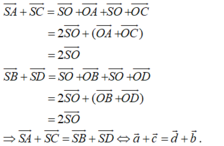
+ Ta có IJ là đường trung bình của tam giác SAB nên IJ// AB// CD
=> IJCD là hình thang. Do đó A đúng.
+ Ta có I B ⊂ S A B I B ⊂ I B C ⇒ S A B ∩ I B C = I B . Do đó B đúng.
+ Ta có J D ⊂ S B D J D ⊂ J B D ⇒ S B D ∩ J B D = J D . Do đó C đúng.
+ Trong mặt phẳng (IJCD), gọi IC và JD cắt nhau tại M .,
=> giao tuyến của mặt phẳng (IAC) và (JBD) là MO
Do đó D sai.
Chọn D.
chào cậu nha^^