Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
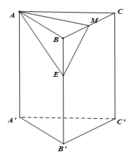
Gọi E là trung điểm của BB' => ME//B'C => (AME)//B'C
![]() = d(C;(AME))
= d(C;(AME))
Vì ![]()
![]()
Gọi h là khoảng cách từ B đến mặt phẳng (AME).
Do tứ diện BAME có BA, BM, BE đôi một vuông góc nên :
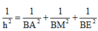
![]()
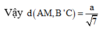

Đáp án D
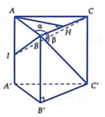
Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()

Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1

Đáp án D
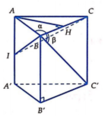
Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()
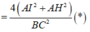
Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1

Đáp án A
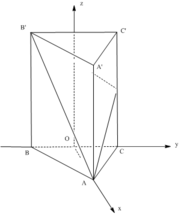
Gắn hệ trục tọa độ Oxyz như hình vẽ
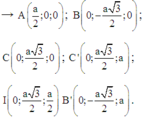
Vecto pháp tuyến của mặt phẳng
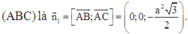
Vecto pháp tuyến của mặt phẳng (AB’I) là
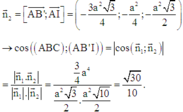

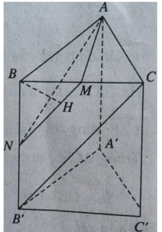
Gọi N là trung điểm của BB’, ta có: CB’ // MN nên CB’ // (AMN). Như vậy
d(BC’, AM) = d(B’, (AMN)) = d(B, (AMN))
(vì B, B’ đối xứng qua N ∈ (AMN)).
Hạ BH ⊥ (AMN), ta có d(B, (AMN)) = BH.
Nhận xét:
Tứ diện B.AMN có ba cạnh BA, BM, BN vuông góc nhau từng đôi một nên
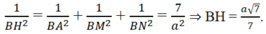

Đáp án B.
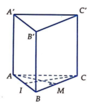
Gọi M là trung điểm của BC ![]() (ABC là tam giác đều)
(ABC là tam giác đều)
![]()
![]() (tam giác ABC đều)
(tam giác ABC đều)
(AM: gọi là đường vuông góc chung của 2 đường thẳng chéo nhau AA', BC).
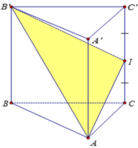


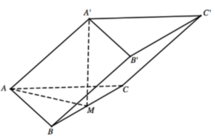

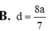
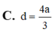

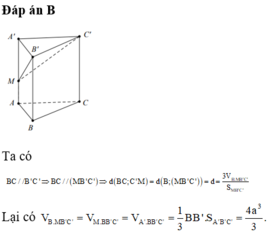

trước hết phải xác định được góc thì mới tính tiếp nhé.kẻ C'H vuông góc A'B' thì ta có C'H vuông góc A'B' và C'H vuông góc BB' thì C'H vuông góc với cả mp AA'B'B và góc là BC'H=60.giờ tính khoảng cách thông qua thể tích chóp MBNC'.tính diện tích MNB và d(C;MNB) là dễ nhất.ra được thể tích thì tính tiếp diện tích BNC'.rồi lắp vào công thức thể tích là ok thôi