Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.

Nhận thấy ∆ ABC là hình chiếu của ∆ AMC' lên mặt phẳng (ABC).
Gọi φ là góc giữa (AMC') và (ABC)
![]()

Ta có 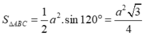
![]()
![]()
=> C'M = 2a

![]()
![]()
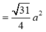
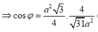
![]()

Đáp án A
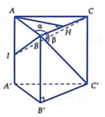
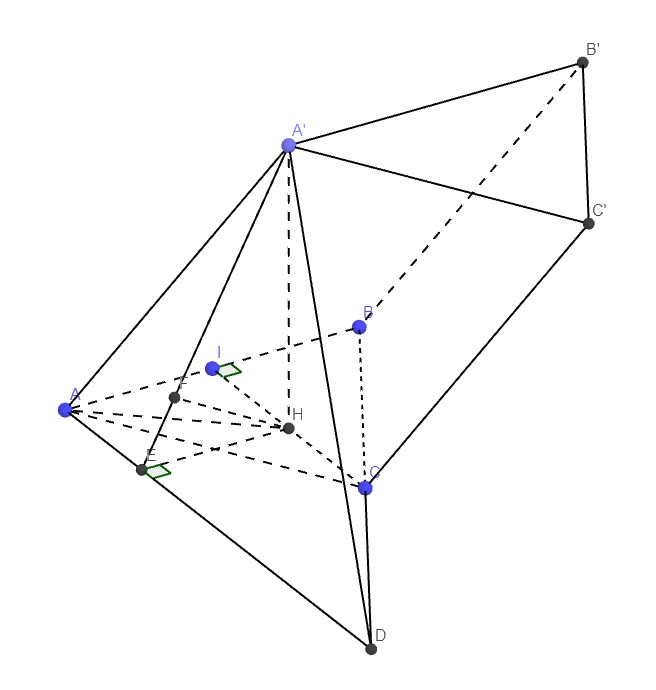
Tam giác ABC là hình chiếu vuông góc của ΔAB′M lên mặt phẳng (ABC).
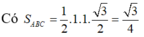
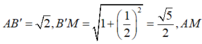
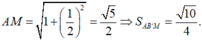
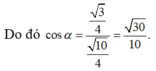

Qua A kẻ đường thẳng song song CI cắt BC kéo dài tại D
\(\Rightarrow CI||\left(A'AD\right)\Rightarrow d\left(A'A;CI\right)=d\left(CI;\left(A'AD\right)\right)=d\left(H;\left(A'AD\right)\right)\)
Từ H kẻ \(HE\perp AD\), từ H kẻ \(HF\perp A'E\)
\(\Rightarrow HF\perp\left(A'AD\right)\Rightarrow HF=d\left(H;\left(A'AD\right)\right)\)
Tứ giác AIHE là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AI=\dfrac{a}{2}\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(A'A\) là (ABC)
\(\Rightarrow\widehat{A'AH}=45^0\)
\(CI=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow IH=\dfrac{1}{2}CI=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow AH=\sqrt{AI^2+IH^2}=\dfrac{a\sqrt{7}}{4}\)
\(\Rightarrow A'H=AH.tan45^0=\dfrac{a\sqrt{7}}{4}\)
Hệ thức lượng:
\(HF=\dfrac{HE.A'H}{\sqrt{HE^2+A'H^2}}=\dfrac{a\sqrt{77}}{22}\)

Đáp án D
Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()

Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1

Đáp án D
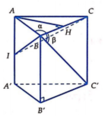
Ta có ![]()
Gọi H là trung điểm của BC.
∆ AHB vuông tại H
![]()
![]()
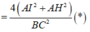
Mà
∆
BIC vuông tại I![]()
Thay vào (*) ta có: tan 2 α + tan 2 β = 1
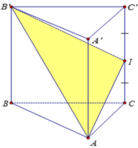

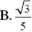
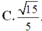
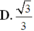
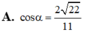
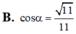
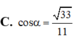
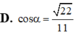
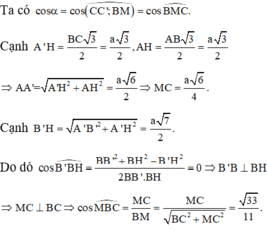
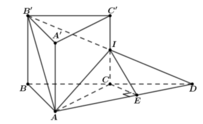
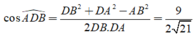
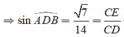
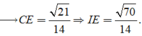
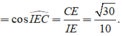
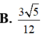
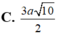
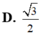




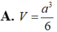
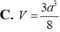
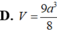

Đáp án A
Gắn hệ trục tọa độ Oxyz như hình vẽ
Vecto pháp tuyến của mặt phẳng
Vecto pháp tuyến của mặt phẳng (AB’I) là