Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) + Tứ giác ABCD là hình bình hành
\(\Rightarrow\hept{\begin{cases}AB//CD\\AO=CO\end{cases}}\)
Tứ giác AECF có : \(\hept{\begin{cases}AE//CF\\AE=CF\end{cases}}\)
=> Tứ giác AECF là hình bình hành
=> AC và EF cắt nhau tại trung điểm của mỗi đường
=> O là trung điểm của EF
=> E đối xứng với F qua O
b) + Tứ giác ABCD là hình bình hành
=> AB = CD => AB - AE = CD - CF
=> BE = DF
Tứ giác BEDF có : \(\hept{\begin{cases}BE=DF\\BE//DF\end{cases}}\)
=> tứ giác BEDF là hình bình hành
=> DE // BF
+ Tứ giác IEKF có : \(\hept{\begin{cases}IE//KF\\IF//KE\end{cases}}\)
=> tứ giác IEKF là hình bình hành
=> IK và EF cắt nhau tại trung điểm mỗi đường
=> O là trung điểm của IK
=> I đối xứng với K qua O

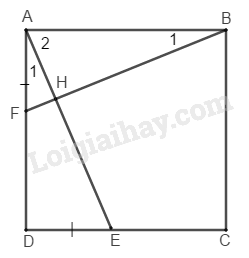
Xét ΔABF và ΔDAE ta có:
AB=DA (gt)
ˆBAF=ˆADE=900
AF=DE (gt)
Do đó: ΔABF=ΔDAE(c.g.c)
⇒BF=AE và ˆB1=ˆA1
Gọi H là giao điểm của AE và BF
ˆBAF=ˆA1+ˆA2=900
⇒ ˆB1+ˆA2=900
Trong ΔABH ta có:
ˆAHB+ˆB1+ˆA2=1800
ˆAHB=1800−(ˆB1+ˆA2)=1800−900=900
Vậy AE⊥BF
a: Xét ΔAED vuông tại A và ΔDFC vuông tại D có
AD=DC
AE=DF
=>ΔAED=ΔDFC
=>FC=DE
b: Xét tứ giác DQPF có
I là trung điểm chung của DP và QF
DP vuông góc DF
=>DQPF là hình thoi