Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o ( định lý tổng 3 góc của 1 tam giác )
90o+50o+\(\widehat{C}\) = 180o
140o+\(\widehat{C}\) = 180o
\(\widehat{C}\) = 180o-140o
\(\widehat{C}\) = 40o
b) Vì KH//AC có góc đồng vị tạo thành
Có \(\widehat{BKH}\) đồng vị với \(\widehat{BAC}\)
=> \(\widehat{BKH}\)=\(\widehat{BAC}\)=90o
=> HK vuông góc với AB
c) Ta có góc C = 40o (câu a)
Ta lại có : \(\widehat{HBK}+\widehat{BKH}+\widehat{BHK}=180^o\) (định lý tổng 3 góc của 1 tam giác)
50o+90o+\(\widehat{BHK}\) = 180o
\(\widehat{BHK}\) = 180o-(50o+90o)
=> \(\widehat{BHK}\) = 40o
Vậy góc BHK = góc C ( 40o=40o )
+ AH _|_ BC => \(\widehat{AHB}\) = 90o
Ta có \(\widehat{AHB}+\widehat{B}+\widehat{BAH}\) = 180o (định lý tổng 3 góc của 1 tam giác)
90o+50o+\(\widehat{AHB}\) = 180o
\(\widehat{AHB}\) = 180o-(90o+50o)
=> \(\widehat{AHB}\) = 40o
Vậy \(\widehat{KHB}=\)\(\widehat{AHB}\) (40o=40o)

a) Xét tam giác AHB có: ^AHB = 90o (AH vuông góc với BC).
=> Tam giác AHB vuông tại H.
=> ^B + ^HAB = 90o.
Mà ^B = 60o (gt).
=> ^HAB = 30o.
b) Xét tam giác HAD có: AD = AH (gt).
=> Tam giác HAD cân tại A.
Mà AI là trung tuyến (I là trung điểm của HD).
=> AI là phân giác ^HAD.
=> ^IAH = ^IAD.
c) Xét tam giác HAK và tam giác DAK có:
+ AH = AD (gt).
+ ^KAH = ^KAD (do ^IAH = ^IAD).
+ AK chung.
=> Tam giác HAK = Tam giác DAK (c - g - c).
=> ^AHK = ^ADK (2 góc tương ứng).
Mà ^AHK = 90o (AH vuông góc với BC).
=> ^ADK= 90o.
=> AD vuông góc KD.
Mà AD vuông góc AB (do tam giác ABC vuông tại góc A).
=> AB // KD (Từ vuông góc đến //).
c) Ta có: ^HAB + ^IAH + ^IAD = 90o (do tam giác ABC vuông tại góc A).
<=> ^HAB + 2^IAH = 90o.
Thay số: 30o + 2^IAH = 90o.
<=> ^IAH = 30o.
=> ^IAH = ^HAB = 30o.
Ta có: HA = HE (gt). => H là trung điểm của AE.
Xét tam giác AKE có:
+ HK là đường cao (AH vuông góc với HK).
+ HK là đường trung tuyến (H là trung điểm của AE).
=> Tam giác AKE cân tại K.
=> ^IAH = ^E (Tính chất tam giác cân).
Mà ^IAH = ^HAB (cmt).
=> ^E = ^HAB. => AB // KE (do 2 góc ở vị trí so le trong).
Mà AB // KD (cmt).
=> 3 điểm D, K, E thẳng hàng (đpcm).

Đề thiếu rồi bạn. Bạn phải nói đề bài cho trước cái gì đã chứ

a) Trong tam giác ABC có góc A + góc B + góc C = 180 độ
\(\Rightarrow\) góc B + góc C = 180 độ - 100 độ = 80 độ
Góc B = (80 + 50) : 2 = 65 (độ)
Góc C = 80 - 65 = 15 (độ)
b) Trong tam giác ABC có góc A + góc B + góc C = 180 độ
\(\Rightarrow\) góc B + góc C = 180 độ - 75 độ = 105 (độ)
Cách 1
Góc B = 105 : (1 + 2) . 2 = 70 (độ)
Góc C = 105 - 70 = 35 (độ)
Cách 2
Gọi số đo góc B, góc C lần lượt là x,y
\(x=2y\Rightarrow\frac{x}{2}=\frac{y}{1}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có
\(\frac{x}{2}=\frac{y}{1}=\frac{x+y}{2+1}=\frac{105}{3}=35\)
\(\Rightarrow\) x = 35.2 = 70; y = 35.1 = 35
Vậy số đo góc B, góc C lần lượt là 70 độ; 35 độ
Bài này chắc không cần vẽ hình đâu

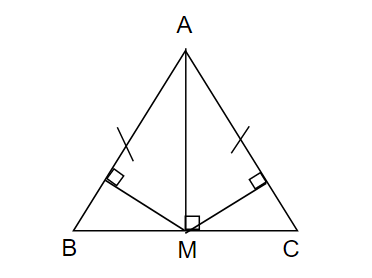
a: Xét ΔAMB vuông tại M và ΔAMC vuông tại M có
AB=AC
AM chung
Do đó: ΔABM=ΔACM
b: Xét ΔABM vuông tại M có \(AB^2=MB^2+AM^2\)
hay MB=9(cm)
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: AH=AK
d: Xét ΔABC có AH/AB=AK/AC
nên HK//BC

a) Ez bạn tự làm nha, mình làm sơ sơ cũng 3-4 cách rồi.:)
b) Tam giác ABC cân tại A có đường p/g góc A xuất phát từ đỉnh đồng thời là đường trung trực nên \(AD\perp BC\). và BD = CD = BC/2
Xét tam giác ABD vuông tại D (chứng minh trên), theo định lí Pythagoras:
\(AB^2=BD^2+DA^2\Leftrightarrow10^2=\frac{BC^2}{4}+DA^2\)
\(=36+DA^2\Rightarrow AD=8\) (cm) (khúc này có tính nhầm gì thì tự sửa lại nha!)
Theo đề bài ta có AB = AC = 10 < BC = 12
Hay AC < BC. Theo quan hệ giữa góc và cạnh đối diện trong tam giác ABC ta có \(\widehat{ABC}< \widehat{BAC}\) (Cái khúc này không chắc, sai thì thôi)
c) Hướng dẫn:
\(\Delta\)EDB = \(\Delta\)FDC (cạnh huyền - góc nhọn)
Suy ra EB = FC. Từ đó suy ra AE = AF.
Suy ra tam giác AEF cân tại A suy ra \(\widehat{AEF}=\frac{180^o-\widehat{A}}{2}\) (1)
Mặt khác tam giác ABC cân tại A nên \(\widehat{ABC}=\frac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) suy ra đpcm

Câu c. lên lớp 8 thì em có thể dùng đường trung bình dễ hơn nhiều nhé.


a: Xét ΔABD vuông tại B và ΔAHD vuông tại H có
AD chung
\(\widehat{BAD}=\widehat{HAD}\)
Do đó: ΔABD=ΔAHD
Suy ra: AB=AH; DB=DH
=>AD là đường trung trực của BH
hay AD⊥BH
b: Xét ΔDAC có \(\widehat{DCA}=\widehat{DAC}\)
nên ΔDAC cân tại D
mà DH là đường cao
nên H là trung điểm của AC
Hình vẽ đâu rồi bạn?