Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
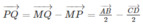
Do đó:
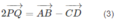
Mặt khác:
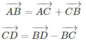
Nên
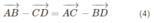
Vì 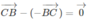
Từ (3) và (4) ta suy ra
![]()
là đẳng thức cần chứng minh.

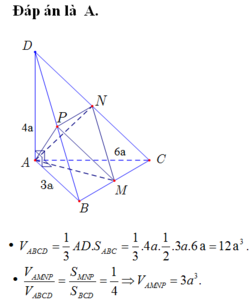
Chọn A
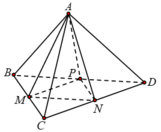
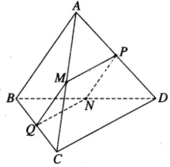
Cách 1: Khối tứ diện ABCD được chia thành bốn tứ diện có thể tích bằng nhau.
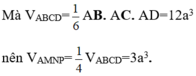
Cách 2:
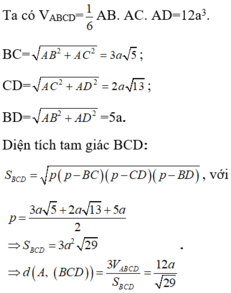
Mà M, N, P là trung điểm các cạnh BC, CD, BD nên hai tam giác BCD và MNP đồng dạng theo tỉ số
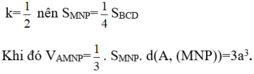

Đáp án B
* Tam giác ABC có MN là đường trung bình nên MN // BC (1)
Tam giác ACD có NP là đường trung bình nên NP // CD (2)
Từ (1) và (2) suy ra: (MNP) song song mp( BCD) hay (MNP) song song mp(Oyz).
* Mà mặt phẳng (Oyz) có 1 vecto pháp tuyến là i → (1; 0; 0) nên mặt phẳng (MNP) có VTPT i → (1; 0; 0).
* Điểm O(0; 0; 0). Gọi I(1; -2; 3) là trung điểm của AO. Suy ra; điểm I thuộc mặt phẳng (MNP).
* Phương trình mặt phẳng (MNP) là:
1(x- 1) + 0(y+ 2) + 0( z- 3) =0 hay x- 1= 0
Chọn B.

Khối chóp C.BDNM có CB là đường cao nên có thể tích ![]() trong đó
trong đó
+ BC = 2a
+ Tứ giác BDNM là hình thang vuông tại B, M do MN là đường trung bình của tam giác ABD nên
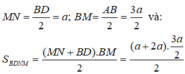
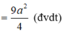
Thể tích của khối chóp C.BDNM là:
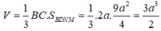


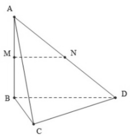

Ta có MPNQ là hình bình hành vì
Do đó
hay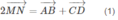
Mặt khác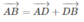
Nên
Vì
Từ (1) và (2) ta có:
là đẳng thức cần chứng minh