Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ BE ⊥ DC ( E ∈ DC ) ⇒ ∠BEC = 90o
AH ⊥ DC ( gt ) ⇒ ∠AHD = 90o
Vì ABCD là hình thang cân nên AD = BC , ∠D = ∠C
Xét ΔAHD và ΔBEC có AD = BC , ∠D = ∠C , ∠AHD = ∠BEC ( =90o )
⇒ ΔAHD = ΔBEC ( g.c.g )
⇒ DH = EC , AH = BE = 8 cm
BE ⊥ DC, AH ⊥ DC ⇒ AH // BE
Xét tứ giác ABEH có AH // BE, AH = BE
⇒ ABEH là hình bình hành ⇒ AB = HE = HC - EC = HC - DH = 12 - DH
Diện tích hình thang ABCD là
\(\dfrac{DC+AB}{2}\).AH=\(\dfrac{DC+12-DH}{2}\).AH = \(\dfrac{HC+12}{2}\).AH=\(\dfrac{12+12}{2}\).8=96cm2
Vậy SABCD = 96cm2

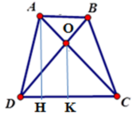
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.48 4 + 8 = 8 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 . 16 3 .8 = 64 3 c m 2
Đáp án: A

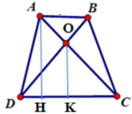
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: AH = 2 S A B C D A B + C D = 2.36 4 + 8 = 6 (cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
O C O A = C D A B = 8 4 = 2 ⇒ O C O A + O C = 2 2 + 1 ⇒ O C A C = 2 3
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
O K A H = O C A C = 2 3 => OK = 2 3 AH => OK = 2 3 .6 = 4(cm)
Do đó S C O D = 1 2 OK.DC = 1 2 .4.8 = 16cm2
Đáp án: C