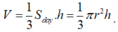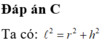
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

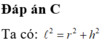

Đáp án B
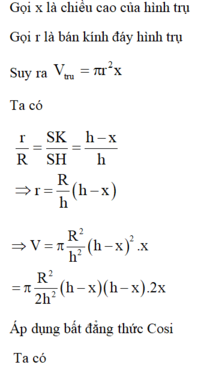
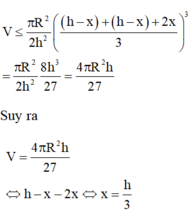
Vậy khi vị trí mặt phẳng α cách đáy hình nón một khoảng h 3 thì khối trụ có diện tích lớn nhất

Đáp án A.
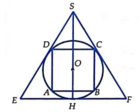
Gọi R là bán kính của hình cầu (S). Bài toán có thể quy về: “Cho đường tròn tâm O, bán kính R ngoại tiếp hình vuông ABCD và nội tiếp ∆ SEF đều” (hình vẽ).
![]()
=>Bán kính đáy và chiều cao của hình trụ (T) lần lượt là
![]()
và ![]()
Thể tích khối trụ là
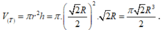
Ta có ∆ SEF đều và ngoại tiếp đường tròn (O) nên O là trọng tâm của ∆ SEF.
Gọi H là trung điểm của EF thì
Hình vuông ABCD nội tiếp đường tròn (O) nên SH = 3OH = 3R![]()
Bán kính đáy và chiều cao của hình nón (N) lần lượt là ![]()
Thể tích khối nón là
![]()
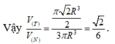

Đáp án D.
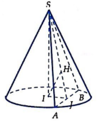
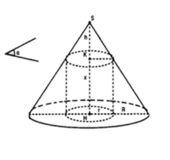
Giả sử hình nón có đỉnh S, đáy là đường tròn tâm I bán kính r, thiết diện đi qua đỉnh là ∆ SAD cân tại S.
Gọi J là trung điểm của AB, ta có
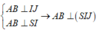
=> (SAB) ⊥ (SIJ)
Trong mặt phẳng (SIJ): Kẻ IH ⊥ (SAB) => IH = d(I;(SAB)) = 24 (cm)
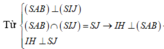
![]()
![]()
![]()
![]()
![]()
![]()
Vậy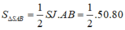 = 2000
c
m
2
= 2000
c
m
2

Đáp án A.
Đường sinh của hình non (N) là ![]()
Diện tích xung quanh của hình nón (N) là S x q = πrl
Diện tích toàn phần của hình nón (N) là
![]()
= πr ( 1 + r )
Thể tích của khối nón (N) là