Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
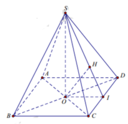
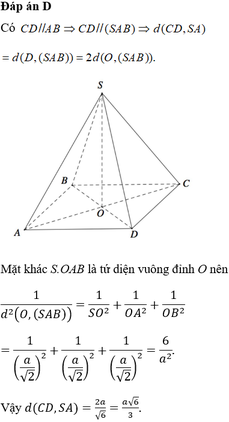
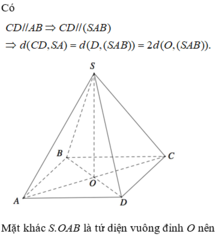
Vì A B / / C D nên d A B ; S C = d A B ; S C D
= d A ; S C D = 2 d O ; S C D = 2 O H , trong đó I là trung điểm của CD và H là hình chiếu vuông góc của O xuống SI.
Ta có: O I = a 2 ; S I = a 2 − a 2 2 = a 3 2 ; S O = a 3 2 2 − a 2 2 = a 2 2
1 O H 2 = 1 O S 2 + 1 O I 2 = 1 a 2 2 2 + 1 a 2 2 = 6 a 2 ⇒ O H = a 6
⇒ d A B ; S C = 2. a 6 = a 6 3

Phương pháp:
- Gắn hệ tọa độ Oxyz với O là tâm hình vuông đáy,

- Xác định tọa độ các điểm cần thiết và tính khoảng cách.
Cách giải:
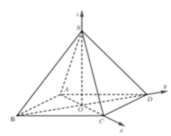
Gắn hệ trục tọa độ như hình vẽ, giả sử SO = b ta có:
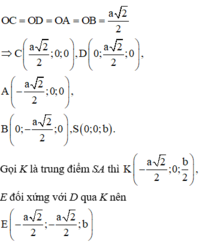

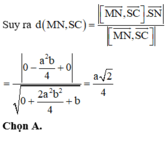

Đáp án C.
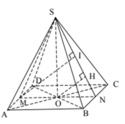
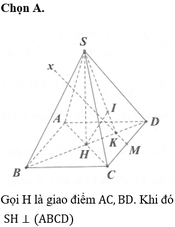
Gọi O chân đường cao hạ từ S xuống mặt đáy ⇒ A C ∩ B D = O .
Dựng O H ⊥ S N (H thuộc SN). Gọi M, N lần lượt là trung điểm của AD và BC. Trong (SMN), kẻ M I // O H (I thuộc SN).
Em có: AD//BC⇒d S B , A D = d A D , S B C = d M , S B C .
Em lại có: S M N ⊥ S B C ⇒ OH ⊥ S B C
Do O H // M I nên MI⊥SBC⇒d M , S B C = M I = 2 O H .
Tam giác SON vuông tại O, đường cao OH nên ta có
1 O H 2 = 1 S O 2 + 1 O N 2 ⇒ O H = a h 4 h 2 + a 2 ⇒ M I = 2 a h 4 h 2 + a 2
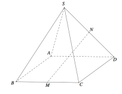
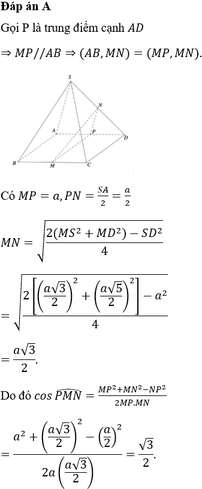
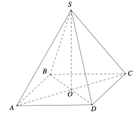

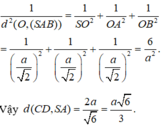

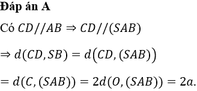
Đáp án C
Gọi O là giao điểm của AC và BD. Ta có AC vuông góc với mặt phẳng (SBD) tại O. Kẻ OH vuông góc với SB, thì OH là khoảng cách cần tìm. Tam giác SOB vuông cân tại O, nên O H = S B 2 = a 2 .