Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(SA=SB=AB\Rightarrow\Delta SAB\) đều
Do SA=SB=SC=SD \(\Rightarrow SO\perp\left(ABCD\right)\)
\(AB||CD\Rightarrow\left(SA;CD\right)=\left(SA;AB\right)=\widehat{SAB}=60^0\)
b.
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\Rightarrow\left(SO;BC\right)=90^0\)
c.
Ta có OM là đường trung bình tam giác SBD \(\Rightarrow OM||SD\)
\(\Rightarrow\left(SD;CM\right)=\left(OM;CM\right)=\widehat{OMC}\)
\(OM=\dfrac{1}{2}SD=a\) ; \(OC=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AB^2+AD^2}=\dfrac{a\sqrt{5}}{2}\)
\(cos\widehat{SBC}=\dfrac{1}{4}\Rightarrow CM=\sqrt{BM^2+BC^2-2BM.BC.cos\widehat{SBC}}=\dfrac{a\sqrt{6}}{2}\)
\(cos\widehat{OMC}=\dfrac{OM^2+CM^2-OC^2}{2OM.CM}=\dfrac{5\sqrt{6}}{24}\)
\(\Rightarrow\widehat{OMC}\simeq59^0\)

Do O là giao điểm 2 đường chéo \(\Rightarrow\) O là trung điểm AC và BD
Tam giác SAC cân tại S \(\Rightarrow SO\) là trung tuyến đồng thời là đường cao
\(\Rightarrow SO\perp AC\) (1)
Tương tự ta có \(SO\perp BD\) (2)
(1); (2) \(\Rightarrow SO\perp\left(ABCD\right)\)
b. Ta có \(AC\perp BD\) nên tam giác OBC vuông tại O
\(\Rightarrow OE=BE=\dfrac{1}{2}BC\) (trung tuyến ứng với cạnh huyền)
Mà \(\widehat{BCD}=\widehat{BAD}=60^0\Rightarrow\Delta BCD\) đều
\(\Rightarrow BD=BC\Rightarrow OB=BE=\dfrac{1}{2}BC\Rightarrow OB=OE=BE\)
\(\Rightarrow\Delta OBE\) đều \(\Rightarrow OF\perp BC\) (trung tuyến tam giác đều đồng thời là đường cao)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOF\right)\Rightarrow\left(SBC\right)\perp\left(SOF\right)\)


bị thừa nha bn tham khảo bn cần thì chép đến phần A thôi nha!

a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)

a: BC vuông góc AB; BC vuông góc SA
=>BC vuông góc (SAB)
b: (BS;(BACD))=(BS;BA)=góc SBA
tan SBA=SA/AB=căn 5/2
=>góc SBA=48 độ
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1
=>góc SCA=45 độ

Bạn coi lại đề, SA vuông góc AD hay SA vuông góc (ABCD)
Nếu SA chỉ vuông góc AD thì không thể chứng minh CD vuông góc SD

Chọn đáp án A
+ Ta có
![]()
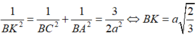
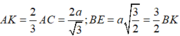
nên K là trọng tâm của tam giác BCD
+ Ta dễ dàng chứng minh được SH ⊥ (BKH) ⇒ SB, (BKH) = SBH
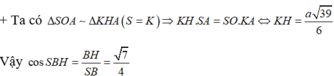
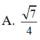
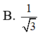
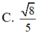
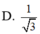
SA=SC
OA=OC
=>SO là trung trực của AC
=>SO vuông góc AC(1)
SB=SD
OB=OD
=>SO là trung trực của BD
=>SO vuông góc BD(2)
Từ (1), (2) suy ra SO vuông góc (ABCD)
=>SO vuông góc CB