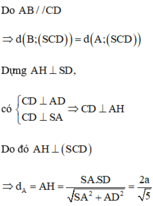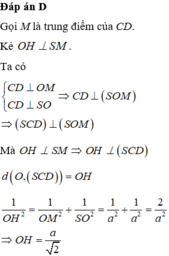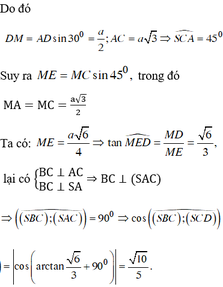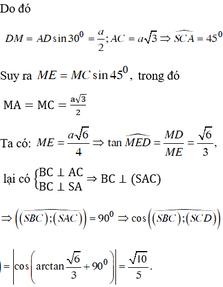Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
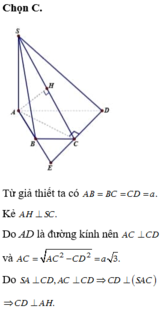
Cách 1: Tư duy tự luận (Tính khoảng cách dựa vào hình chiếu)

Ta có
A B // C D A B ⊄ S C D C D ⊂ S C D ⇒ A B // S C D ⇒ d B , S C D = d A ; S C D
Lại có C D ⊥ A D , A D ⊂ S A D C D ⊥ S A , S A ⊂ S A D A D ∩ S A = A ⇒ C D ⊥ S A D .
Trong mặt phẳng (SAD) : Kẻ A H ⊥ S D , H ∈ S D thì C D ⊥ A H .
Suy ra A H ⊥ A C D ⇒ A H = d A ; S C D = d B ; S C D .
Δ S A D vuông tại A nên
1 A H 2 = 1 S A 2 + 1 A D 2 = 1 2 a 2 + 1 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .
Cách 2: Tư duy tự luận (Tinh khoảng cách qua công thức thể tích)
Thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a 2 = 2 a 3 3 (đvtt)
Do S Δ B C D = 1 2 S A B C D ⇒ V S . B C D = 1 2 V S . A B C D = a 3 3 (đvtt).
Ta có C D ⊥ S A D (xem lại phần chứng minh ở cách 1) ⇒ C D ⊥ S D ⇒ Δ S C D vuông tại D. Suy ra
S Δ S C D = 1 2 S D . C D = 1 2 S A 2 + A D 2 . C D = 1 2 . a . 2 a 2 + a 2 = a 2 5 2
(đvdt)
Mặt khác
V S . B C D = V B . S C D = 1 3 d B ; S C D . S Δ S C D ⇒ d B ; S C D = 3 V S . B C D S Δ S C D = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .

Đáp án D
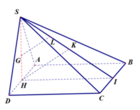
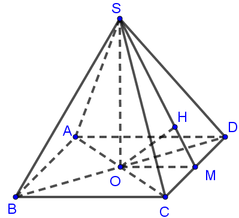
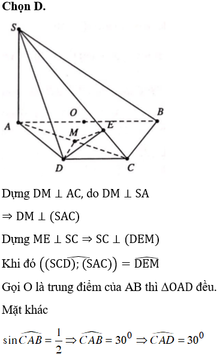
Gọi H, I , theo thứ tự là trung điểm AD,BC
G là tâm đường tròn nội tiếp tam giác đều
SAD nên G cũng là trọng tâm tam giác SAD.
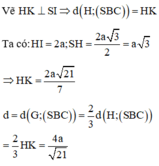

Đáp án C.
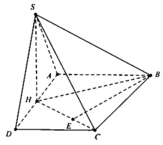
Ta có SAD là tam giác đều nên S H ⊥ A D
Mặt khác S A D ⊥ A B C D ⇒ S H ⊥ A B C D .
Dựng B E ⊥ H C ,
do B E ⊥ S H ⇒ B E ⊥ S H C
Do đó d = B E = 2 a 6 ; S H = a 3 ; A D = 2 a
Do S C = a 15 ⇒ H C = S C 2 − S H 2 = 2 a 3 .
Do S A H B + S C H D = 1 2 a A B + C D = S A B C D 2
suy ra V S . A B C D = 2 V S . H B C = 2 3 . S H . S B C H
= 3 2 a 3 . B E . C H 2 = 4 a 3 6 .

Đáp án C
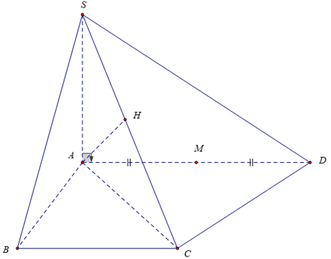
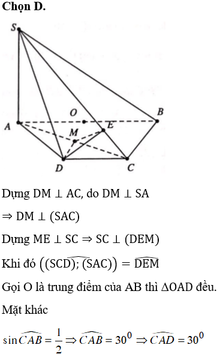
Theo dữ kiện đề bài cho, dễ dàng chứng minh được ΔACD vuông tại cân C và A C = A D 2 = a 2 .
C D ⊥ A C C D ⊥ S A ⇒ C D ⊥ S A C ⇒ S A C ⊥ S C D
Mà S A C ∩ S C D = S C , từ A kẻ A H ⊥ S C . Khi đó d A ; S C D = A H .
Tam giác SAC vuông tại
A: 1 A H 2 = 1 S A 2 + 1 A C 2 = 1 a 2 + 1 2 a 2 = 3 2 a 2 ⇒ d A ; S C D = A H = a 2 3
Mặt khác: A D ∩ S C D = D và M là trung điểm AD nên:
d M ; S C D d A ; S C D = M D A D = 1 2 ⇒ d M ; S C D = 1 2 d A ; S C D = a 6 6