K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
16 tháng 7 2019
Đáp án B
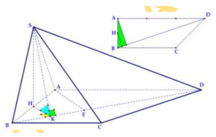
Mặt phẳng cách đều 5 điểm là mặt phẳng mà khoảng cách từ 5 điểm đó đến mặt phẳng là bằng nhau.
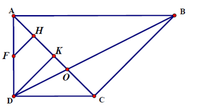
Có 5 mặt phẳng thỏa mãn là:
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SBC .
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SAD .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SAB .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SCD .
+ Mặt phẳng đi qua trung điểm của SA,SB,SC,SD.
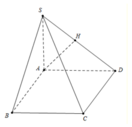
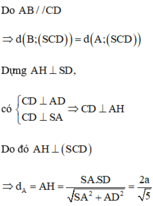


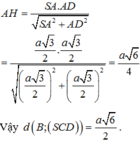



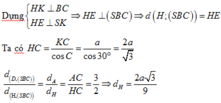
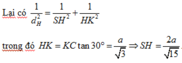


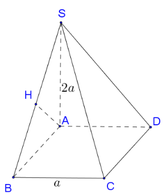

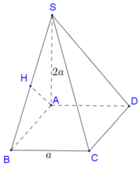
Đáp án D
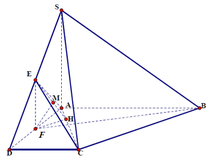
Cách 1: Tư duy tự luận (Tính khoảng cách dựa vào hình chiếu)
Ta có
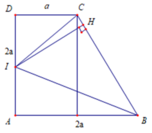
A B // C D A B ⊄ S C D C D ⊂ S C D ⇒ A B // S C D ⇒ d B , S C D = d A ; S C D
Lại có C D ⊥ A D , A D ⊂ S A D C D ⊥ S A , S A ⊂ S A D A D ∩ S A = A ⇒ C D ⊥ S A D .
Trong mặt phẳng (SAD) : Kẻ A H ⊥ S D , H ∈ S D thì C D ⊥ A H .
Suy ra A H ⊥ A C D ⇒ A H = d A ; S C D = d B ; S C D .
Δ S A D vuông tại A nên
1 A H 2 = 1 S A 2 + 1 A D 2 = 1 2 a 2 + 1 a 2 = 5 4 a 2 ⇒ A H = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .
Cách 2: Tư duy tự luận (Tinh khoảng cách qua công thức thể tích)
Thể tích khối chóp S.ABCD là V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a 2 = 2 a 3 3 (đvtt)
Do S Δ B C D = 1 2 S A B C D ⇒ V S . B C D = 1 2 V S . A B C D = a 3 3 (đvtt).
Ta có C D ⊥ S A D (xem lại phần chứng minh ở cách 1) ⇒ C D ⊥ S D ⇒ Δ S C D vuông tại D. Suy ra
S Δ S C D = 1 2 S D . C D = 1 2 S A 2 + A D 2 . C D = 1 2 . a . 2 a 2 + a 2 = a 2 5 2
(đvdt)
Mặt khác
V S . B C D = V B . S C D = 1 3 d B ; S C D . S Δ S C D ⇒ d B ; S C D = 3 V S . B C D S Δ S C D = 2 a 5
Vậy khoảng cách từ điểm B đến mặt phẳng (SCD) là d = 2 a 5 5 .