Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.

Xác định được
![]()
Vì M là trung điểm SA nên
![]()
Kẻ AK ⊥ DM và chứng minh được AK ⊥ (CDM) nên
![]()
Trong tam giác vuông MAD tính được
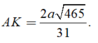


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy
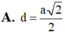
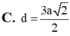
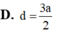

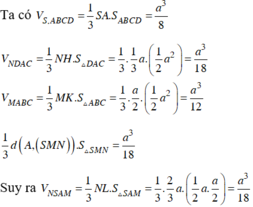
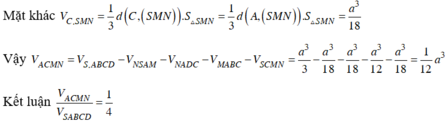
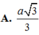
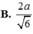
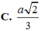
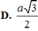
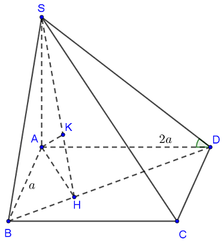
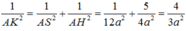
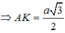
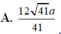
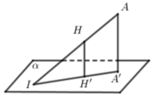
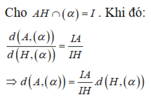
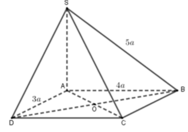

Nối DM và AB kéo dài cắt nhau tại E
Do BM song song và bằng 1 nửa AD \(\Rightarrow BM\) là đường trung bình tam giác ADE
\(\Rightarrow AE=2BE\Rightarrow d\left(B;\left(SMD\right)\right)=\dfrac{1}{2}d\left(A;\left(SMD\right)\right)\)
Lại có: \(\left\{{}\begin{matrix}BN\cap\left(SMD\right)=S\\NS=\dfrac{1}{3}BS\end{matrix}\right.\) \(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{3}d\left(B;\left(SMD\right)\right)=\dfrac{1}{6}d\left(A;\left(SMD\right)\right)\)
Từ A kẻ AF vuông góc MD (F thuộc MD), từ A kẻ AH vuông góc SF (H thuộc SF)
\(\Rightarrow AH\perp\left(SMD\right)\Rightarrow AH=d\left(A:\left(SMD\right)\right)\)
Hệ thức lượng trong tam giác vuông ADE:
\(\Rightarrow AF=\dfrac{AD.AE}{DE}=\dfrac{AD.2AB}{\sqrt{AD^2+\left(2AB\right)^2}}=\dfrac{8a\sqrt{17}}{17}\)
\(SA=\sqrt{SD^2-AD^2}=a\sqrt{21}\)
Hệ thức lượng: \(AH=\dfrac{SA.AF}{\sqrt{SA^2+AF^2}}=...\)
\(\Rightarrow d\left(N;\left(SMD\right)\right)=\dfrac{1}{6}AF=...\)