
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

![]()
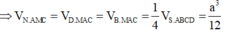

1: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>(SAB) vuông góc (SBC)

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)