Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(SA=x;SB=y\)
\(S_{\Delta SAB}=\dfrac{1}{2}SA.SB=\dfrac{xy}{2}\)
\(V=\dfrac{SA.SB.SC}{6}.\sqrt{1+2.cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{axy}{6}\)
\(\Rightarrow d\left(C;\left(SAB\right)\right)=\dfrac{3V}{S}=\dfrac{axy}{2.\dfrac{xy}{2}}=a\)

\(S_{\Delta ACD}=\dfrac{1}{2}AC.AD.sin\widehat{CAD}=\dfrac{a^2\sqrt{3}}{4}\)
\(V=\dfrac{AB.AC.AD}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290^0-cos^260^0-cos^2120^0}=\dfrac{a^3\sqrt{2}}{12}\)
\(\Rightarrow d\left(B;\left(ACD\right)\right)=\dfrac{3V}{S}=\dfrac{a\sqrt{6}}{3}\)

\(AB=\sqrt{SA^2+SB^2}=a\sqrt{2}\)
\(AC=\sqrt{SA^2+SC^2-2SA.SC.cos120^0}=\sqrt{3}\)
\(BC=\sqrt{SB^2+SC^2-2SB.SC.cos60^0}=a\)
\(\Rightarrow AB^2+BC^2=AC^2\Rightarrow\Delta ABC\) vuông tại B
Gọi H là hình chiếu vuông góc của S lên (ABC) \(\Rightarrow\) H là tâm đường tròn ngoại tiếp ABC (do SA=SB=SC)
\(\Rightarrow\) H trùng trung điểm AC
Gọi M là trung điểm SA \(\Rightarrow MH||SC\Rightarrow\) góc giữa SC và (SAB) bằng góc giữa MH và (SAB)
Gọi N là trung điểm AB \(\Rightarrow HN\perp AB\Rightarrow AB\perp\left(SHN\right)\)
Trong mp (SHN), kẻ \(HK\perp SN\Rightarrow HK\perp\left(SAB\right)\)
\(\Rightarrow\widehat{KMH}\) là góc giữa SC và (SAB)
\(SH=\sqrt{SA^2-\left(\dfrac{AC}{2}\right)^2}=...\)
\(MH=\dfrac{1}{2}SA=...\) (trung tuyến ứng với cạnh huyền)
\(NH=\dfrac{1}{2}BC=...\) (đường trung bình)
\(\Rightarrow\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{NH^2}\Rightarrow HK=...\)
\(\Rightarrow sin\widehat{KMH}=\dfrac{HK}{MH}=...\)

Đáp án D
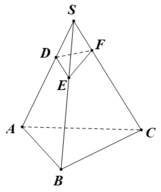
Gọi D, E, F lần lượt trên SA, SB, SC sao cho SD = SE = SF = 1 => S.DEF là hình chóp đều cạnh a
Ta có 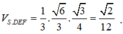
Lại có 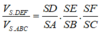
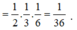
Vậy 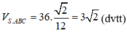

Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)
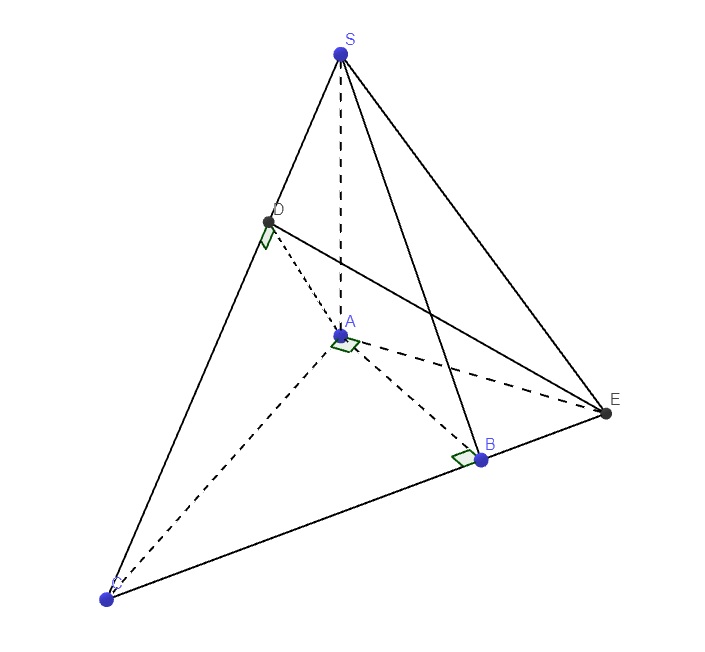
\(V=\dfrac{a.a\sqrt{3}.a\sqrt{2}}{6}.\sqrt{1+2cos90^0.cos60^0.cos120^0-cos^290-cos^260-cos^2120}=\dfrac{a^3\sqrt{3}}{6}\)