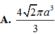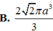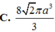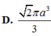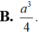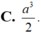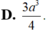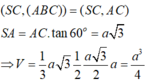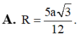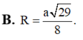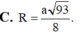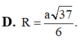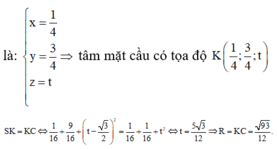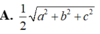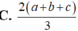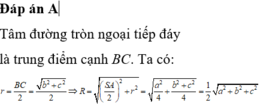Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Áp dụng công thức tìm nhanh bán kính mặt cầu ngoại tiếp hình chóp R 2 = x 2 + r 2 với
r là bán kính đường tròn ngoại tiếp đa giác đáy
x = S O 2 - r 2 2 h : S là đỉnh hình chóp , O là tâm đường tròn ngoại tiếp đa giác đáy, h là chiều cao hình chóp
Cụ thể vào bài toán:
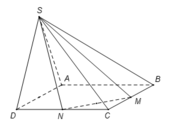
Đáy là tam giác CMN vuông tại C
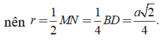
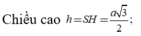
Tâm O của đường tròn ngoại tiếp tam giác CMN là trung điểm MN
Áp dụng công thức đường trung tuyến trong tam giác HMN tính được H O 2 = 5 a 2 8
Trong tam giác vuông SHO có
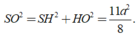
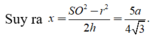
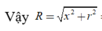
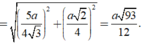

Đáp án B.
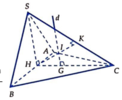
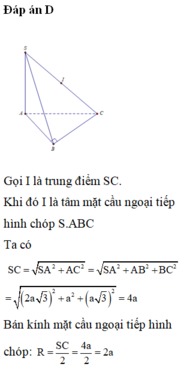
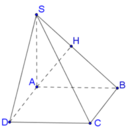
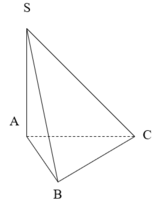
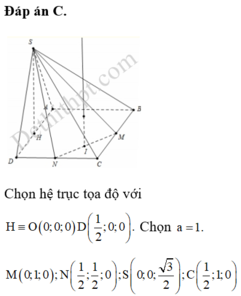
Gọi H là trung điểm AB, G là trọng tâm tam giác ABC, K là trung điểm SC.
Ta có: ![]()
SH = SC => HK là trung trực SC. Qua O kẻ trục d//SH => d ⊥ (ABC)
Gọi
![]()
=> I là tâm mặt cầu ngoại tiếp hình chóp SABC
Ta có
![]()
Xét ∆ HIG vuông tại G:
![]()
Vậy thể tích khối cầu ngoại tiếp hình chóp
![]()

a.
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

Gọi K là trung điểm của SA
=>KM//SC
=>SC//(KMB)
d(SC;BM)=d(S;(KBM))=SK/SA*d(A;(KBM))=d(A;(KBM))
=>ΔABC đều
=>BM vuông góc AC
=>BM vuông góc (SAC)
Kẻ AQ vuông góc KM
=>AQ vuông góc (KMB)
=>d(A;(KMB))=AQ
\(SC=\sqrt{9a^2+4a^2}=a\sqrt{13}\)
KM=1/2SC=a*căn 3/2
=>\(AQ=\dfrac{3\sqrt{13}}{13}\)
=>d(BM;SC)=3*căn 13/13