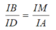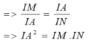Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. vì ABCD là hình bình hành => MB//CD
theo hệ quả của định lý Ta-lét, ta có: tam giác NMB ~ tam giác NDC
vì AD//CN (ABCD là hbh)
=> \(\dfrac{AK}{KC}\)= \(\dfrac{KD}{KN}\)
góc AKD = góc NKC (đối đỉnh)
=> tam giác AKD ~ tam giác CKN (c.g.c)

Mình làm luôn câu b cho nhé:
Tg AKD đồng dạng với tg CKN (câu a)
=>\(\frac{AK}{CK}=\frac{KD}{KN}\)(đ/n) (1)
ABCD là hình bình hành => AB song song với CD.
=>Tg CDK đồng dạng với tg AMK ( hệ quả của đ/lí Talet)
=>\(\frac{CK}{AK}=\frac{DK}{MK}\)(đ/n) (2)
Từ (1),(2)=>\(\frac{KD}{KN}=\frac{KM}{KD}\left(=\frac{AK}{CK}\right)\)
=>KD\(^2\)=KM.KN

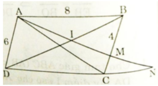
a) AD // BC (gt)![]()
b) Xét ΔAMB và ΔNAD có:
∠BAM = ∠ AND (so le trong, AB // CD)
∠ABM = ∠ADN (góc đối của hình bình hành)
⇒ ΔAMB ∼ ΔNAD (g.g)
c) ΔAMB ∼ ΔNAD (cmt)
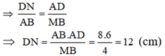
Do đó: CN = DN – DC = 12 – 8 = 4 (cm)
d) Do AB //CD nên theo hệ quả định lí Ta-lét, ta có
![]()
Tương tự, do AD // BM nên