Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có a = 1- √5 < 0 nên hàm số đã cho nghịch biến trên R.
b) Khi x = 1 + √5 ta có:
y = (1 - √5).(1 + √5) - 1 = (1 - 5) - 1 = -5
c) Khi y = √5 ta có:
√5 = (1 - √5)x - 1
=> √5 + 1 = (1 - √5)x
![]()
(hoặc trục căn thức ở mẫu như dưới đây:
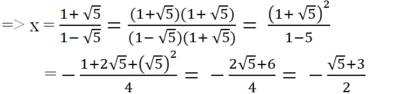

Vẽ hình:
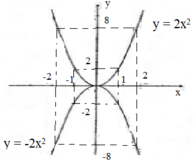
a) Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.
b) Đồ thị hàm số y = a x 2 là đường cong (đặt tên là parabol) đi qua gốc tọa độ nhận trục tung Oy làm trục đối xứng.
Nếu a > 0 thì đồ thị nằm trên trục hoành, điểm O là điểm thấp nhất đồ thị (gọi là đỉnh parabol).
Nếu a < 0 thì đồ thị nằm bên dưới trục hoành, điểm O là điểm cao nhất của đồ thị.

Vẽ hình:
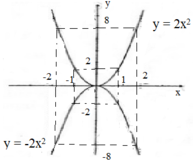
Nếu a > 0 thì hàm số đồng biến khi x > 0, nghịch biến khi x < 0
Với x = 0 thì hàm số đạt giá trị nhỏ nhất bằng 0. Không có giá trị nào của hàm số để đạt giá trị lớn nhất.
Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
Hàm số đạt giá trị lớn nhất y = 0 khi x = 0 . Không có giá trị bào của x để hàm số đạt giá trị nhỏ nhất.

a) hàm số bậc nhất -2m-4\(\ne\)0<=>m\(\ne-2\)
b)hàm số nghịch biến\(-2m-4< 0\Leftrightarrow m>-2\)
\(a,f\left(x\right)=\left(-2m-4\right)x+1\) bậc nhất \(\Leftrightarrow-2m-4\ne0\Leftrightarrow m\ne-2\)
\(b,f\left(x\right)=\left(-2m-4\right)x+1\) nghịch biến \(\Leftrightarrow-2m-4< 0\Leftrightarrow-2m< 4\Leftrightarrow m>-2\)

a)
đường thẳng (d1) song song với đường thẳng (d2) khi :
a = a' và b khác b'
suy ra :
\(m-1=3\) \(\Leftrightarrow m=4\)
vậy đường thẳng (d1) song song với đường thẳng (d2) khi m = 4
 Câu hỏi 2 (0.25 điểm)
Câu hỏi 2 (0.25 điểm)