Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(y'=4x^3+2x\)
a. \(y=1\Rightarrow x^4+x^2+1=1\Rightarrow x^2\left(x^2+1\right)=0\Rightarrow x=0\Rightarrow y'=0\)
Phương trình tiếp tuyến: \(y=0\left(x-0\right)+1\Leftrightarrow y=1\)
b. \(y'\left(-1\right)=-6\)
Phương trình tiếp tuyến: \(y=-6\left(x+1\right)+3\)

\(y'=8x^3-8x\)
a. Đường thẳng \(x-48y+1=0\) có hệ số góc \(\dfrac{1}{48}\) nên tiếp tuyến có hệ số góc \(k=-48\)
\(\Rightarrow8x^3-8x=-48\Rightarrow x^3-x+6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-2x+3\right)=0\Rightarrow x=-2\)
\(y'\left(-2\right)=47\)
Phương trình tiếp tuyến: \(y=-48\left(x+2\right)+47\)
b. Gọi tiếp điểm có hoành độ \(x_0\)
Phương trình tiếp tuyến: \(y=\left(8x_0^3-8x_0\right)\left(x-x_0\right)+2x^4_0-4x^2_0-1\) (1)
Do tiếp tuyến qua A:
\(\Rightarrow-3=\left(8x_0^3-8x_0\right)\left(1-x_0\right)+2x_0^4-4x^2_0-1\)
\(\Leftrightarrow3x_0^4-4x_0^3-2x_0^2+4x_0-1=0\)
\(\Leftrightarrow\left(x_0-1\right)^2\left(3x_0^2+2x_0-1\right)=0\Rightarrow\left[{}\begin{matrix}x_0=1\\x_0=-1\\x_0=\dfrac{1}{3}\end{matrix}\right.\)
Có 3 tiếp tuyến thỏa mãn. Thay lần lượt các giá trị \(x_0\) bên trên vào (1) là được

- Hàm số đã cho xác định với ∀x ≠ 1.
- Ta có:
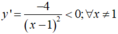
- Gọi M ( x 0 ; y 0 ) là tọa độ tiếp điểm, suy ra phương trình tiếp tuyến của (C):
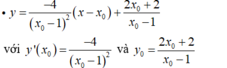
- Tiếp tuyến tạo với 2 trục tọa độ lập thành một tam giác cân nên hệ số góc của tiếp tuyến bằng ± 1. Mặt khác: y ' ( x 0 ) < 0 , nên có: y ' ( x 0 ) = - 1 .
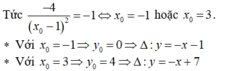
- Vậy, có 2 tiếp tuyến thỏa mãn đề bài: y = -x - 1; y = -x + 7.
Chọn D

f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11

Với x 0 = 1 thì y 0 = 2016 và f’(1) = 0.
- Do đó, phương trình tiếp tuyến tại điểm có hoành độ x= 1 là
y = 0(x- 1) + 2016 hay y = 2016.

\(y'=\dfrac{-1}{\left(x-1\right)^2}\)
Gọi tiếp tuyến qua điểm \(M\left(a;b\right)\) thuộc (C) có dạng:
\(y=\dfrac{-1}{\left(a-1\right)^2}\left(x-a\right)+\dfrac{2a-1}{a-1}\)
\(\Leftrightarrow x+\left(a-1\right)^2y-2a^2+2a-1=0\)
Áp dụng công thức khoảng cách:
\(\dfrac{\left|1+2\left(a-1\right)^2-2a^2+2a-1\right|}{\sqrt{1+\left(a-1\right)^4}}=\sqrt{2}\)
\(\Leftrightarrow\left|2a-2\right|=\sqrt{2}.\sqrt{1+\left(a-1\right)^4}\)
\(\Leftrightarrow2\left(a-1\right)^2=1+\left(a-1\right)^4\)
\(\Leftrightarrow\left[\left(a-1\right)^2-1\right]^2=0\Rightarrow a=...\)
b.
Vẫn từ công thức khoảng cách trên:
\(d=\dfrac{\left|2a-2\right|}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2\sqrt{\left(a-1\right)^2}}{\sqrt{1+\left(a-1\right)^4}}=\dfrac{2}{\sqrt{\dfrac{1}{\left(a-1\right)^2}+\left(a-1\right)^2}}\)
\(d\le\dfrac{2}{\sqrt{2\sqrt{\dfrac{\left(a-1\right)^2}{\left(a-1\right)^2}}}}=\sqrt{2}\)
Vậy \(d_{max}=\sqrt{2}\) khi tiếp tuyến trùng với các tiếp tuyến câu a
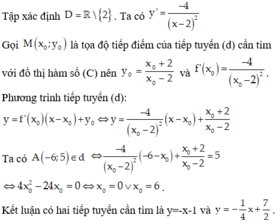
y=-6x-3
Gọi N(x_0;y_0)N(x0;y0) là tiếp điểm của tiếp tuyến đã cho.
Phương trình tiếp tuyến dd có dạng: y = (4x_0^3+2x_0)(x-x_0)+x_0^4+x_0^2+1y=(4x03+2x0)(x−x0)+x04+x02+1.
M \in dM∈d nên 3 = (4x_0^3+2x_0)(-1-x_0)+x_0^4+x_0^2+1 \Leftrightarrow 3x_0^4+4x_0^3+x_0^2+2x_0+2=03=(4x03+2x0)(−1−x0)+x04+x02+1⇔3x04+4x03+x02+2x0+2=0
\Leftrightarrow (x_0+1)^2(3x_0^2-2x_0+2) = 0 \Leftrightarrow x_0 = -1 \Rightarrow y_0 = 3⇔(x0+1)2(3x02−2x0+2)=0⇔x0=−1⇒y0=3 và y'(x_0)=-6y′(x0)=−6.
Phương trình tiếp tuyến là y = -6x-3.y=−6x−3.