Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

f'(x)=y'=-3x^2+2x
f'(2)=-3*2^2+2*2=-3*4+4=-8
f(2)=-2^3+2^2-1=-8-1+4=-9+4=-5
y=f(2)+f'(2)(x-2)
=-5+(-8)(x-2)
=-8x+16-5
=-8x+11

a. \(y'\left(x_0\right)=-2x_0+3\)
b. phương trình tiếp tuyến tại x0 =2 là
\(y=y'\left(x_0\right)\left(x-x_0\right)+y_0=-\left(x-2\right)+0\text{ hay }y=-x+2\)
c.\(y_0=0\Rightarrow\orbr{\begin{cases}x_0=1\\x_0=2\end{cases}\Rightarrow PTTT\orbr{\begin{cases}y=x-1\\y=-x+2\end{cases}}}\)
d. vì tiếp tuyến vuông góc với đường thẳng có hệ số góc bằng 1 nên tiếp tuyến có hệ số góc = -1
hay \(-2x_0+3=-1\Leftrightarrow x_0=2\Rightarrow PTTT:y=-x+2\)

Đặt \(y=f(x)=x^3+2x^2+x-1 \)
\(f'(x)=3x^2+4x+1\)
Phương trình tiếp tuyến của đồ thị hàm số y tại M là:
\(y=f'(x_m)(x-x_m)+f(x_m)=f'(1)(x-1)+f(1)=8(x-1)+3=8x-5 \)

- Gọi x 0 ; y 0 là tọa độ tiếp điểm.
- Ta có:
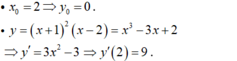
- Vậy phương trình tiếp tuyến cần tìm là:
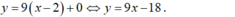
Chọn D.

\(y'=\dfrac{\left(5x-1\right)'\left(x+2\right)-\left(5x-1\right)\cdot\left(x+2\right)'}{\left(x+2\right)^2}\)
\(=\dfrac{5\left(x+2\right)-5x+1}{\left(x+2\right)^2}=\dfrac{5x+10-5x+1}{\left(x+2\right)^2}=\dfrac{11}{\left(x+2\right)^2}\)
\(f\left(-1\right)=\dfrac{-5-1}{-1+2}=-6\)
f'(-1)=11/(-1+2)^2=11
Phương trình tiếp tuyến tại M(-1;-6) là:
y=11(x+1)+(-6)=11x+11-6=11x+5
Với x = –2 ta có: y = –3 và y'(2) = 2.