K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HQ
2 tháng 8 2019
\(A\cap B=\left(0;4\right)\)
\(A\cup B=\left[-2;5\right]\)
\(B\backslash A=\left[4;5\right]\)
\(C_RA=R\backslash A=\left(-\infty;-2\right)\cup[4;+\infty)\)
NT
1
30 tháng 5 2022
\(C_R^{A\cap B}\)=R\(-2;1]=\((-\infty;-2]\cup\left(1;+\infty\right)\)
\(C_R^{A\cup B}\)=R\(-\(\infty\);3)=[3;+\(\infty\))
14
1
11 tháng 10 2021
\(A\cup B=\left(-2;2\right)\)
\(A\cap B=\left\{0\right\}\)
\(A\B=\left(-2;0\right)\)
14
1
13 tháng 10 2021
\(A\cup B=\left(-2;2\right)\\ A\cap B=\left\{0\right\}\\ A\B=\left(-2;0\right)\)
14
1
11 tháng 10 2021
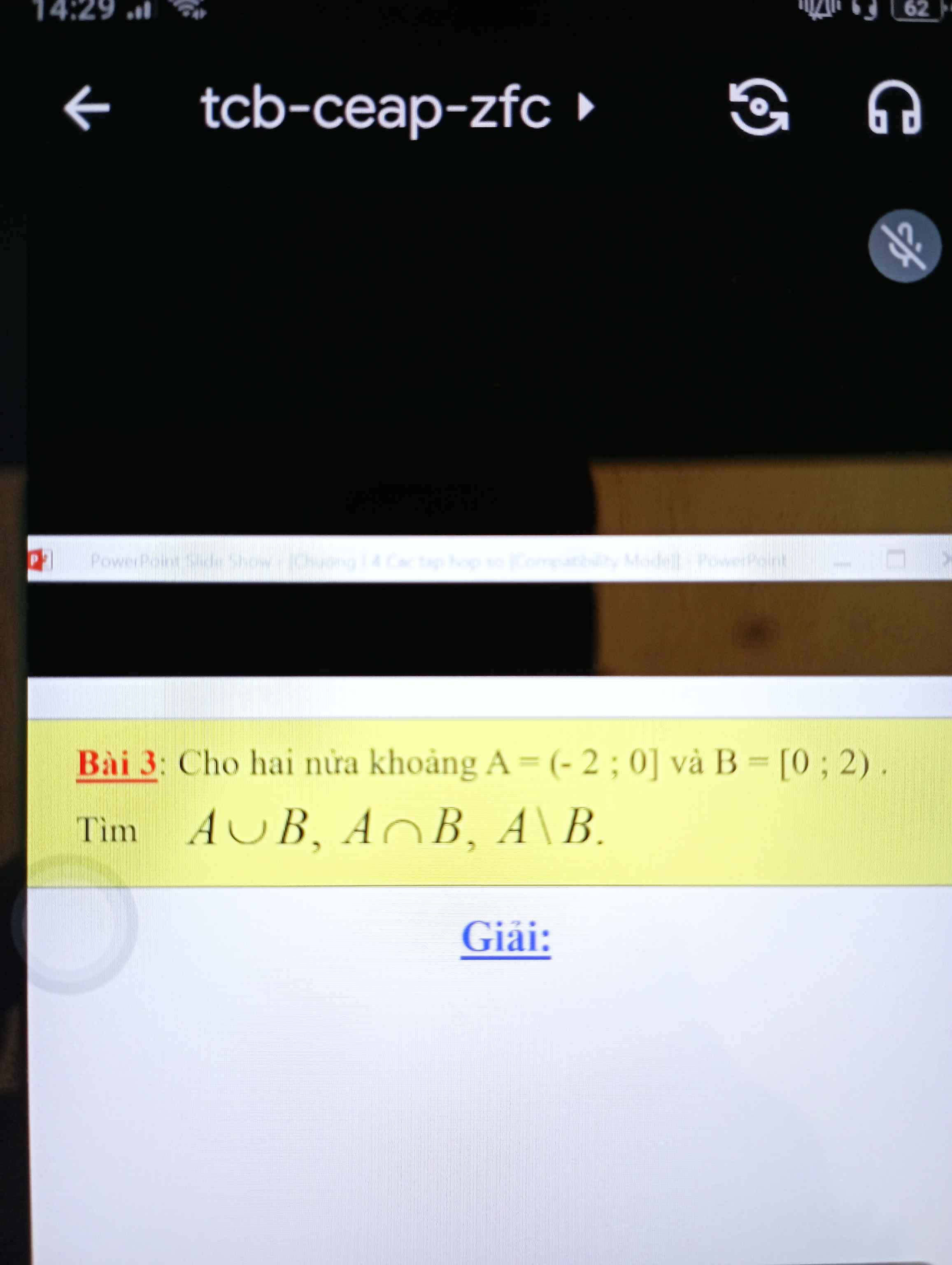
\(A\cup B=\left(-2;2\right)\)
\(A\cap B=0\)
A\B=(-2;0)
AH
Akai Haruma
Giáo viên
13 tháng 10 2021
Lời giải:
\(A\cup B=(-2;2)\)
\(A\cap B=\left\{0\right\}\)
\(A\setminus B=(-2;0)\)
Về hình vẽ trên trục số thì đơn giản rồi. Bạn có thể tự vẽ.
PN
0
KL
1
