Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Điền vào ô trống:
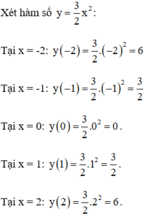
Vậy ta có bảng:
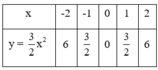
Tương tự như vậy với hàm số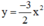 
. Ta có bảng:
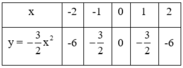
+ Vẽ đồ thị hàm số:
Trên mặt phẳng lưới lấy các điểm A(-2; 6);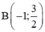 
; O(0; 0); 
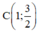; D(2; 6).
Nối các điểm trên theo một đường cong ta được parabol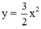 
Lấy các điểm A’ (-2; -6);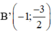 
; O(0; 0); 
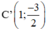; D’(2; -6).
Nối các điểm trên theo một đường cong ta được parabol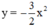 
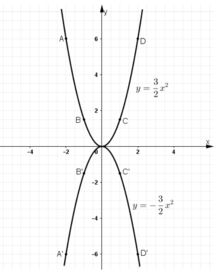
Nhận xét: Đồ thị hàm số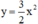 
và 
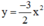đối xứng nhau qua trục Ox.
a: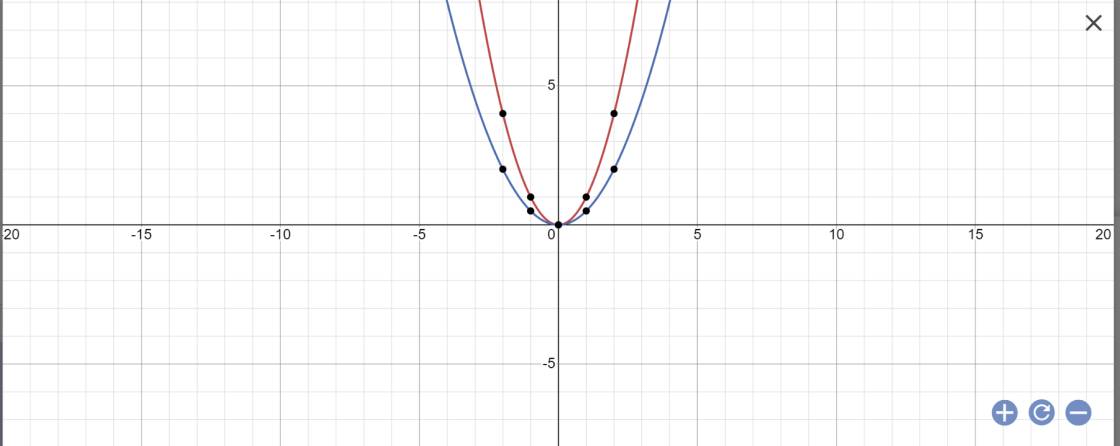 
b: Khi x=2 thì y=1/2*2^2=2
=>A(2;2)
Khi x=2 thì y=2^2=4
=>B(2;4)
c: Tọa độ A' là:
\(\left\{{}\begin{matrix}x_{A'}=-x_A=-2\\y_{A'}=y_A=2\end{matrix}\right.\)
Vì f(-2)=1/2*(-2)^2=2
nên A' thuộc (P1)
Tọa độ B' là:
\(\left\{{}\begin{matrix}x_{B'}=-x_B=-2\\y_{B'}=y_B=4\end{matrix}\right.\)
Vì f1(-2)=(-2)^2=4
nên B' thuộc y=x^2
Câu 2:
c) Phương trình hoành độ giao điểm của (P) và (d) là:
\(\dfrac{1}{2}x^2=2x+6\)
\(\Leftrightarrow\dfrac{1}{2}x^2-2x-6=0\)
\(\Leftrightarrow x^2-4x-12=0\)
\(\Leftrightarrow x^2-4x+4=16\)
\(\Leftrightarrow\left(x-2\right)^2=16\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=4\\x-2=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=6\\x=-2\end{matrix}\right.\)
Thay x=6 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot6^2=18\)
Thay x=-2 vào (P), ta được:
\(y=\dfrac{1}{2}\cdot\left(-2\right)^2=\dfrac{1}{2}\cdot4=2\)
Vậy: Tọa độ giao điểm của (P) và (d) là (6;18) và (-2;2)
Câu 3:
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{-\left(-2\right)}{1}=2\\x_1\cdot x_2=\dfrac{c}{a}=\dfrac{-1}{1}=-1\end{matrix}\right.\)
Ta có: \(P=x_1^3+x_2^3\)
\(=\left(x_1+x_2\right)^3-3\cdot x_1x_2\left(x_1+x_2\right)\)
\(=2^3-3\cdot\left(-1\right)\cdot2\)
\(=8+3\cdot2\)
\(=8+6=14\)
Vậy: P=14
a) Đồ thị được vẽ như hình bên.
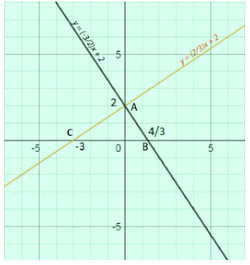
b) Vì M thuộc đồ thị y = y = 
x + 2 và tung độ của nó là y = 1 nên x + 2= 1.
Suy ra x = -1,5.
Vậy M(-1,5; 1).
Vì N thuộc đồ thị y = - 
x + 2 và tung độ của N là y = 1 nên - x + 2 = 1.
Suy ra x = .
Vậy N(; 1).
Bài giải:
a) Đồ thị được vẽ như hình bên.
b) Vì M thuộc đồ thị y = y = x + 2 và tung độ của nó là y = 1 nên x + 2= 1.
Suy ra x = -1,5.
Vậy M(-1,5; 1).
Vì N thuộc đồ thị y = - x + 2 và tung độ của N là y = 1 nên - x + 2 = 1.
Suy ra x = .
Vậy N(; 1)
Hàm số \(y=\sqrt{3-m}\left(x+5\right)\) là hàm số bậc nhất khi \(\sqrt{3-m}\ne0\)
\(\Leftrightarrow3-m\ne0\)
\(\Leftrightarrow m\ne3\)
Tọa độ giao điểm của hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) là nghiệm của hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x-2-\dfrac{3}{2}x+2=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x=0\\y=\dfrac{1}{2}x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=\dfrac{1}{2}\cdot0-2=-2\end{matrix}\right.\)
Vậy: Hai đồ thị hàm số \(y=\dfrac{1}{2}x-2\) và \(y=\dfrac{3}{2}x-2\) có tọa độ giao điểm là (0;-2)
\(y=\sqrt{3-m}.\left(x+5\right)\) là hàm số bậc nhất \(\Leftrightarrow\sqrt{3-m}\ne0\Leftrightarrow m\ne3\)
Lập PT hoành độ ta có:
\(\dfrac{1}{2}x-2=\dfrac{3}{2}x-2\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y=\dfrac{1}{2}.0-2=-2\)
=> Tọa độ (0;-2)
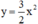
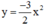
Bài giải:
Thực hiện phép tính và điền vào chỗ trống ta được bảng sau:
Vẽ đồ thị:
Nhận xét: Đồ thị của hai hàm số đối xứng với nhau qua trục Ox.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-36-sgk-toan-9-tap-2-c44a5695.html#ixzz4dH45gBuO