Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
MB,MA là tiếp tuyến
nên MB=MA
Xét (O') cos
MA,MC là tiếp tuyến
nên MA=MC=>MA=BC/2
Xét ΔABC có
AM la trung tuyến
AM=BC/2
Do đó; ΔABC vuông tại A
b: Gọi H là trung điểm của OO'
Xét hình thang OBCO' có
M,H lần lượt là trung điểm của BC,OO'
nên MH là đường trung bình
=>MH//BO//CO'
=>MH vuông góc với BC
=>BC là tiếp tuyến của (H)

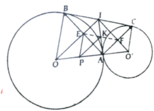
a, Chứng minh tứ giác AEIF là hình chữ nhật và K là trung điểm AI
b, Có IE.IO = I B 2 = B C 2 4 và IF.IO' = I C 2 = B C 2 4
=> 2.(IE.IO+IF.IO') = A B 2 + A C 2
c, PK Là đường trung bình của ∆OAI và là trung trực của EA
Ta có ∆PEK = ∆PAK nên P E K ^ = P A K ^
Vậy P E K ^ = 90 0 => đpcm
d, ∆ABC:∆IOO’ => S A B C S I O O ' = B C O O ' 2 => S A B C = S I O O ' . B C 2 O O ' 2
mà BC = 2AI'; OO' = 2a; S O I O ' = 1 2 . 2 a . I A = a . I A => S A B C = I A 2 a
I A 2 = R R ' ⩽ R + R ' 2 2 = a 2 => IA lớn nhất bằng a khi R=R’