Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.

Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
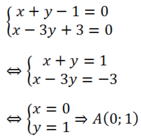
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
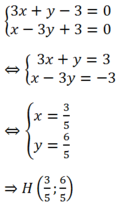
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
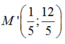
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 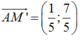
=> vectơ pháp tuyến 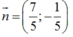
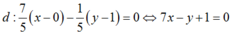

ĐÁP ÁN C
Ta có: 6 2 = − 3 − 1 ≠ 4 3 nên d1 // d2.
Ta có: d 2 : 2 x − y + 3 = 0 ⇔ 6 x − 3 y + 9 = 0
Do d1 // d2. nên khoảng cách hai đường thẳng d1và d2 chính là đường kính của đường tròn.
Suy ra, bán kính đường tròn tiếp xúc với hai đường thẳng d1;d2 là
R = 1 2 d d 1 , d 2 = 1 2 9 − 4 6 2 + − 3 2 = 5 6

Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn

Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
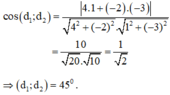

Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
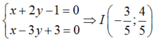
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
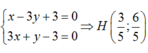
Phương trình đường thẳng
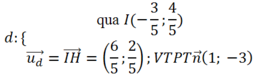
có dạng:
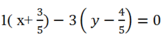
hay x-3y + 3= 0

M thuộc (d1) nên M(1-2t;1+t)
Theo đề, ta có: d(M;d2)=d(M;d3)
=>\(\dfrac{\left|\left(1-2t\right)\cdot3+\left(1+t\right)\cdot4-4\right|}{\sqrt{3^2+4^2}}=\dfrac{\left|\left(1-2t\right)\cdot4+\left(1+t\right)\cdot\left(-3\right)+2\right|}{\sqrt{4^2+\left(-3\right)^2}}\)
=>|-6t+3+4t+4-4|=|4-8t-3t-3+2|
=>|-2t+3|=|-11t+3|
=>-2t+3=-11t+3 hoặc -2t+3=11t-3
=>t=0 hoặc t=6/13
=>M(1;1); M(1/13; 19/13)

Đường thẳng song song với d1 và d2 là:
(d3): 2x - 3y + c (với c khác 1 và c khác 1,5)