Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1) Xét hai tam giác ODN và OEM có:
OD = OE (gt)
\(\widehat{O}\): góc chung
OM = ON (gt)
Vậy \(\Delta ODN=\Delta OEM\left(c-g-c\right)\)
Suy ra: EM = DN (hai cạnh tương ứng)
2) Ta có: DM = OM - OD
EN = ON - OE
Mà OM = ON (gt)
OD = OE (gt)
\(\Rightarrow\) DM = EN
Xét hai tam giác DMK và ENK có:
DM = EN (cmt)
\(\widehat{M_1}=\widehat{N_1}\left(\Delta ODN=\Delta OEM\right)\)
EM = DN (cmt)
Vậy \(\Delta DMK=\Delta ENK\left(c-g-c\right)\)
Suy ra: KM = KN (hai cạnh tương ứng).

a/ Xét t/g OAD và t/g OBC cos
AO = OB
\(\widehat{xOy}\) : chung
OD = OC
=> t/g OAD = t/g OBC
=> AD = BC
b/ Không rõ đề.
c/ Có
OC = ODOA = OB
=> AC = BD
Có \(\widehat{OAD}=\widehat{OBE}\) (do t/g OAD = t/g OBC)
=> \(180^o-\widehat{OAD}=180^o-\widehat{OBE}\)
=> \(\widehat{CAD}=\widehat{CBD}\)
Xét t/g AEC và t/g BED có
\(\widehat{CAD}=\widehat{CBD}\)
AC = BD\(\widehat{OCB}=\widehat{ODA}\)
=> t/g AEC = t/g BED (g.c.g)
=> AE = BE
Xét t/g OAE và t/g OBE có
OA = OB
AE = BEOE : chung
=> t/g OAE = t/g OBE
=> ^xOE = ^yOe
=> OE là pg góc xOy

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Xét ΔACD và ΔBDC có
AC=BD
\(\widehat{ACD}=\widehat{BDC}\)
CD chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{EAC}=\widehat{EBD}\)
Xét ΔEAC và ΔEBD có
\(\widehat{EAC}=\widehat{EBD}\)
AC=BD
\(\widehat{ECA}=\widehat{EDB}\)
Do đó: ΔEAC=ΔEBD

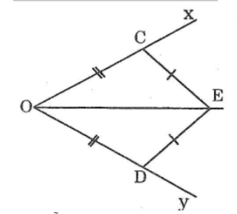
Xét ΔCOE và ΔDOE. Ta có:
OE cạnh chung
OD = OC (giả thiết)
DE=CE ( bán kính 2 cung tròn có bán kính bằng nhau)
Suy ra: ΔCOE= ΔDOE(c.c.c)
Vậy : ∠(COE) =∠(DOE) (hai góc tương ứng)
Vì điểm E nằm trong góc xOy nên tia OE nằm giữa OC và OD (2)
Từ (1) và (2) suy ra: OE là tia phân giác của góc DOC hay OE là tia phân giác của góc xOy


+) Xét t/g ODN và t/g OEM có:
OD = OE (gt)
góc ODN = góc OEM =90 độ
góc O chung
=> t/g ODN = t/g OEM (g-c-g)
=> DN = EM (hai cạnh tương ứng)
=> góc DMK = góc KNE và OD = OE mà OM = ON => DM = EN
+) Xét t/g KDM và t/g KEN có:
góc KDM = KEN = 90 độ
DM = EN (cmt)
góc DMK = góc KNE (cmt)
=> t/g KDM = t/g KEN (g-c-g)
=> KM = KN (hai cạnh tương ứng)