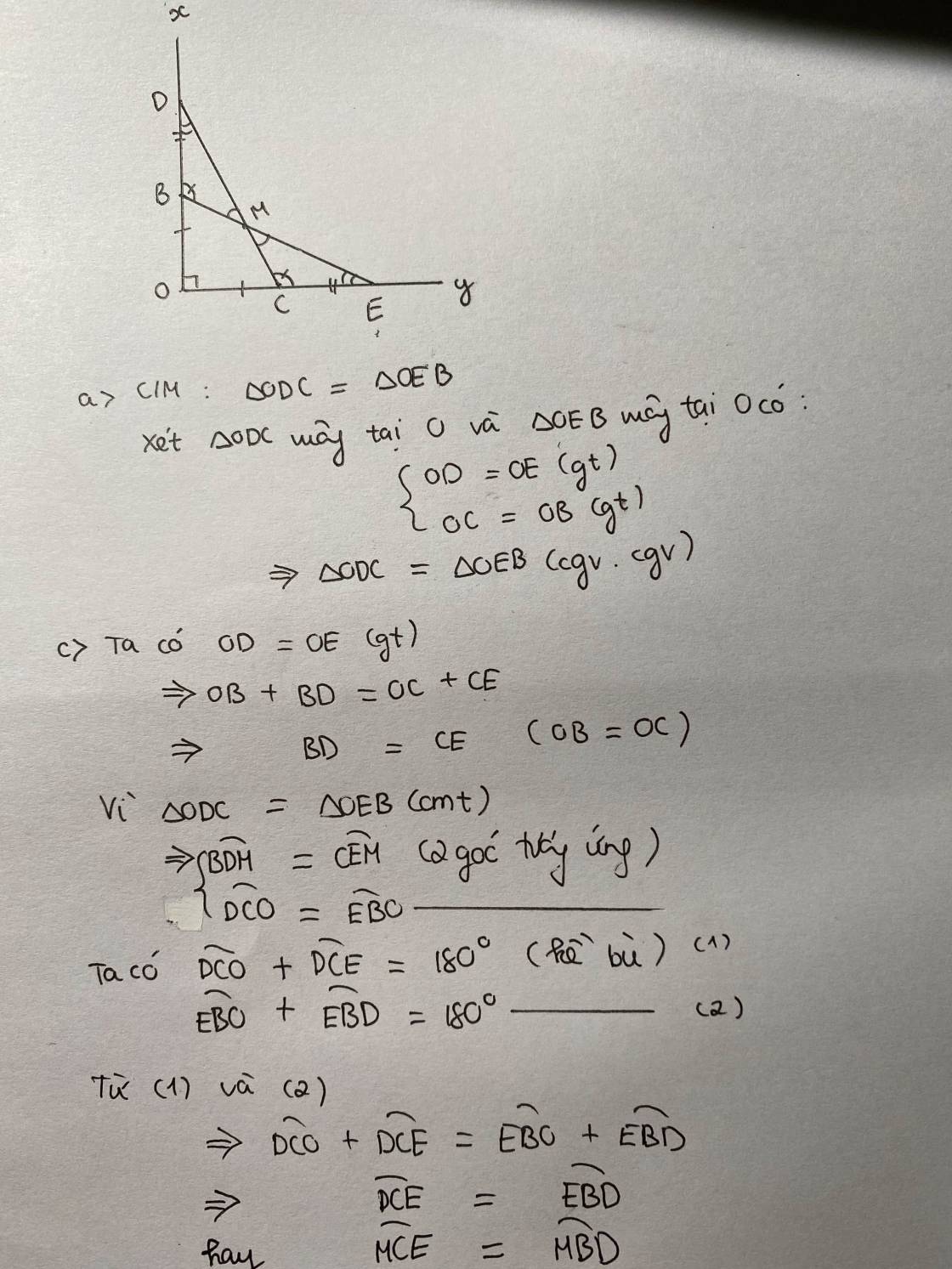Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔODC và ΔOBE có
OD=OB
\(\widehat{O}\) chung
OC=OE
Do đó: ΔODC=ΔOBE
Câu b và c đề sai rồi bạn

Chép lại đề: (vì đề của bạn có chút sai sót)
Cho \(\widehat{xOy}\) khác góc bẹt. Lấy A, B thuộc Ox sao cho OA < OB. Lấy C, D thuộc Oy sao cho OC = OA; OD = OB. Gọi E là giao điểm của AD và BC. CMR:
a, AD = BC
b, Tam giác AEB = tam giác CED
c, OE là tia phân giác của \(\widehat{xOy}\)
Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OBC có
OA = OC (GT)
\(\widehat{O}\): góc chung
OB = OD (GT)
Vậy tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng) (đpcm)
b/ Xét tam giác AEB và tam giác CED có:
\(\widehat{B}\)=\(\widehat{D}\) (vì tam giác OAD = tam giác OBC) (1)
OA = OC; OB = OD => AB = CD (2)
Ta có: \(\Delta\)OAD = \(\Delta\)OBC
=> \(\widehat{OAD}\)=\(\widehat{OCB}\) (2 góc tương ứng) (*)
Ta có: \(\widehat{OAD}\)+\(\widehat{DAB}\)=1800 (kề bù) (**)
\(\widehat{OCB}\) + \(\widehat{BCD}\) = 1800 (kề bù) (***)
Từ (*), (**), (***) \(\Rightarrow\)\(\widehat{DAB}\)=\(\widehat{BCD}\)(3)
Từ (1), (2), (3) => tam giác AEB = tam giác CED (g.c.g) (đpcm)
c/ Xét tam giác OBE và tam giác ODE có:
OB = OD (GT)
OE: cạnh chung
BE = EC (vì tam giác AEB = tam giác CED)
Vậy tam giác OBE = tam giác ODE (c.c.c)
=> \(\widehat{BOE}\)=\(\widehat{DOE}\) (2 góc tương ứng)
=> OE là phân giác góc xOy (đpcm)
Vậy OE là tia phân giác \(\widehat{xOy}\)

ΔAEB = ΔCED ⇒ EA = EC (hai cạnh tương ứng)
ΔOAE và ΔOCE có
OA = OC
EA = EC
OE cạnh chung
⇒ ΔOAE = ΔOCE (c.c.c)
⇒  (hai góc tương ứng)
(hai góc tương ứng)
Vậy OE là tia phân giác của góc xOy.

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC

a: Xét ΔOAD và ΔOBC có
OA=OB
\(\widehat{O}\) chung
OD=OC
Do đó: ΔOAD=ΔOBC
Suy ra: AD=BC
b: Ta có: ΔOAD=ΔOBC
nên \(\widehat{OAD}=\widehat{OBC}\)
\(\Leftrightarrow180^0-\widehat{OAD}=180^0-\widehat{OBC}\)
hay \(\widehat{EAB}=\widehat{ECD}\)
Xét ΔEAB và ΔECD có
\(\widehat{EAB}=\widehat{ECD}\)
AB=CD
\(\widehat{EBA}=\widehat{EDC}\)
Do đó: ΔEAB=ΔECD
c: Ta có: ΔEAB=ΔECD
nên EB=ED
Xét ΔOEB và ΔOED có
OE chung
EB=ED
OB=OD
Do đó: ΔOEB=ΔOED
Suy ra: \(\widehat{BOE}=\widehat{DOE}\)
hay OE là tia phân giác của góc xOy