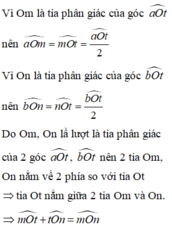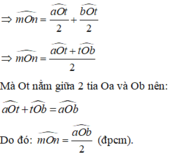Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

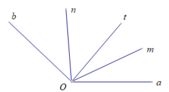
ta có \(Om\) là phân giác của \(\widehat{aOt}\) => \(\widehat{mOt}=\frac{\widehat{aOt}}{2}\)
tương tự ta có \(\widehat{nOt}=\widehat{\frac{bOt}{2}}\)
=> \(\widehat{mOt}+\widehat{nOt}=\frac{\widehat{aOt}+\widehat{bOt}}{2}=\widehat{\frac{aOb}{2}}\)
mà \(Ot\) nằm giữa \(Om\) và \(On\)
=> \(\widehat{mOn}=\widehat{mOt}+\widehat{nOt}=\widehat{\frac{aOb}{2}}\) (ĐPCM)

Theo tính chất 2 tia pg ngoài và 1 tia pg trong đồng quy tại một điểm => AK là phân giác ngoài của gocs BAC =>CAK = 40 độ => BAK = 140độ nhé

a/ ob nằm giữa oa ,oc vì aoc > aob
b/ vì on là pg aoc
=> aon = noc = aoc : 2 = 150 : 2 = 75 độ
c/ vì om là pg aob
=> aom = mob = aob : 2 = 50 : 2 = 25 độ
vì aon > aom
=> om nằm giữa oa ,on
vì thế: aom + mon = aon
=> mon = aon - aom = 75 - 25 = 50 độ
d/ vì aob < aon
=> ob nằm giữa oa ,on
vì thế: aob + bon = aon
=> bon = aon - aob = 75 - 50 = 25 độ
vì mon > bon
=. ob nằm giữa om ,on
vì thế: mob + bon = mon
=> mob = mon - bon = 50 - 25 = 25 độ
=> mob = bon = 25 độ
từ hai điều in đậm trên, chứng minh ob là pg mon

(Xin lỗi mình không điền các điểm được)
1) OM là tia phân giác của góc AOB suy ra tia OM nằm giữa hai tia OA và OB ; MOB = AOM = \(\frac{1}{2}\) AOB. (1)
Do đó : MOB < AOB.
ON là tia phân giác của góc BOC suy ra tia ON nằm giữa hai tia OB và OC ; BON = CON = \(\frac{1}{2}\) BOC. (2)
Do đó : BON < BOC.
2) Từ (1) và (2), ta có:
MON = BOM + BON = \(\frac{1}{2}\) AOB + \(\frac{1}{2}\)BOC = \(\frac{1}{2}\)(AOB + BOC) = \(\frac{1}{2}\) AOC.
Vậy suy ra điều phải chứng minh.
2/ theo đề: om là pg aob
=> aom = mob = 1/2 aob
on là pg cob
=> bon = noc = 1/2 cob
=> mob + bon = mon= 1/2 cob + boa ( = 1/2 coa)