
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4: \(\left|x^3-64\right|+\left|15-4y\right|=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x^3-64=0\\15-4y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{15}{4}\end{matrix}\right.\)
6: |7x-11|>5
=>7x-11>5 hoặc 7x-11<-5
=>7x>16 hoặc 7x<6
=>x>16/7 hoặc x<6/7
8: |2x+12|<4
=>2x+12>-4 và 2x+12<4
=>2x>-16 và 2x<-8
=>-8<x<-4

a,\(f\left(-4\right)=2.\left(-4\right)^3-3.\left(-4\right)=2.\left(-64\right)+12=-128+12=-116\)
\(f\left(-2\right)=2.\left(-2\right)^3-3.\left(-2\right)=2.\left(-8\right)+6=-16+6=-10\)
\(f\left(0\right)=2.0^3-3.0=2.0-0=0-0=0\)
\(f\left(\dfrac{2}{3}\right)=2.\left(\dfrac{2}{3}\right)^3-3.\left(\dfrac{2}{3}\right)=2.\dfrac{8}{27}-2=\dfrac{16}{27}-2=\dfrac{-38}{27}\)
b,
\(f\left(x\right)=25\rightarrow y=25\)
Ta có : \(x^3-2=25\)
\(\rightarrow x^3=27\)
\(\Rightarrow x=3\) ( Vì 27 = \(3^3\) )

( bn xem lại đầu bài giúp mk nha! )
ta có: \(f_{\left(x\right)}=3x^{1800}.x^{200}+5+4x^{101}.x^{99}+3x^{15}.x^5+2.x^2+2000\)
\(f_{\left(x\right)}=3x^{2000}+4x^{200}+3x^{20}+2x^2+2005\)
mà \(3x^{2000}\ge0;4x^{200}\ge0;3x^{20}\ge0;2x^2\ge0\)
\(\Rightarrow3x^{2000}+4x^{200}+3x^{20}+2x^2\ge0\)
mà \(2005>0\Rightarrow3x^{2000}+4x^{200}+3x^{20}+2x^2+2005>0\)
=> Không tồn tại giá trị của x để f(x) =0

f(x)=x^3-2x^2+3x+1
g(x)=x^3+x^2-5x+3
a: f(-1/3)=-1/27-2/9-1+1=-1/27-6/27=-7/27
g(-2)=-8+4+10+3=17-8=9
b: f(x)-g(x)=x^3-2x^2+3x+1-x^3-x^2+5x-3
=x^2+8x-2
f(x)+g(x)
=x^3-2x^2+3x+1+x^3+x^2-5x+3
=2x^3-x^2-2x+4
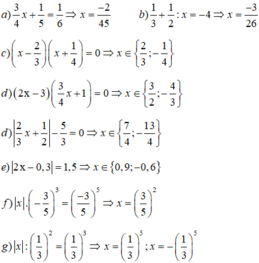
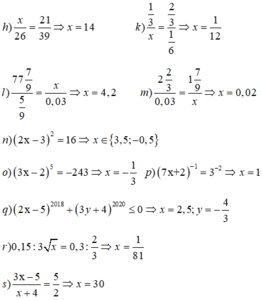
Ta có:
x + 3 = 0
=> x = -3
Tại x = -3, giá trị của f(x) là:
f(x) = x15 + 3x14 + x + 2018
=(-3)15 + 3.(-3)14 + (-3) + 2018
= (-3)14 . [(-3) + 3] -3 + 2018
= (-3)14 . 0 - 3 + 2018
= 0 - 3 + 2018
= -3 + 2018
= 2015
Vậy f(x) = 2015