Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
Phương trình tổng quát của đường thẳng d đi qua M(2;-3) và nhận n → = 3 ; - 2 làm vecto pháp tuyến có dạng:
3(x - 2) - 2(y + 3) = 0 ⇔ 3x - 2y - 12 = 0

Lưu ý: Nếu 2 đường thẳng vuông góc với nhau thì vecto chỉ phương của đường thẳng này là vecto pháp tuyến của đường thẳng kia và ngược lại
22/ \(\left(d\right)\perp\left(\Delta\right)\Rightarrow\overrightarrow{u_d}=\overrightarrow{n_{\Delta}}=\left(3;-4\right)\)
23/ \(\left(d\right)\perp\left(\Delta\right)\Rightarrow\overrightarrow{n_d}=\overrightarrow{u_{\Delta}}=\left(-2;-5\right)\)

chọn A
đường thẳng đi qua \(2\) điểm \(A\left(-3;2\right)\) và \(B\left(1;4\right)\) có \(VTCP\) là :
\(\overrightarrow{AB}\) \(=\left(4;2\right)\) hoặc \(\overrightarrow{u}\) \(\left(2;1\right)\)

Đáp án: A
Δ: x - 2y + 3 = 0 có 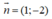
Ta thấy: (4;-2).(1;-2) = 4.1 + (-2).(-2) = 4 + 4 = 8 ≠ 0
Nên (4;-2) không phải là vecto chỉ phương của Δ