Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

CHỌN C vì :
Hệ số góc của đường thẳng d có vectơ chỉ phương u→ = (-1; \(\sqrt{3}\)) là:

1.
Phương trình đường thẳng có dạng:
\(2\left(x-2\right)-1\left(y-1\right)=0\Leftrightarrow2x-y-3=0\)
2.
Do d song song \(\Delta\) nên nhận \(\left(2;-3\right)\) là 1 vtpt
Phương trình: \(2\left(x-1\right)-3\left(y-1\right)=0\Leftrightarrow2x-3y+1=0\)
3.
Do đường thẳng vuông góc d nên nhận \(\left(3;4\right)\) là 1vtpt
\(3\left(x-2\right)+4\left(y-3\right)=0\Leftrightarrow3x+4y-18=0\)

Đáp án C
Phương trình đường thẳng d là.
y = 2( x-2) – 5
Hay 2x-y -9 =0

chọn A
đường thẳng đi qua \(2\) điểm \(A\left(-3;2\right)\) và \(B\left(1;4\right)\) có \(VTCP\) là :
\(\overrightarrow{AB}\) \(=\left(4;2\right)\) hoặc \(\overrightarrow{u}\) \(\left(2;1\right)\)

Chọn B.
Giả sử đường thẳng d với hệ số góc là k = -2 có dạng: y = -2x + b
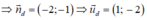
Phương trình tham số đi qua D(4; 1) nhận 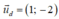 là VTCP là:
là VTCP là:
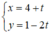

a) (d) đi qua M(-2;3) và có VTCP \(\overrightarrow{u}\)=(1;-4)
(d)\(\left\{{}\begin{matrix}quaM\left(-2;3\right)\\\overrightarrow{u}=\left(1;-4\right)\end{matrix}\right.\)
ptts (d) : Δ \(\left\{{}\begin{matrix}x=-2+1t
\\y=3-4t\end{matrix}\right.\) (t∈R)
b) (d) đi qua 2 điểm A(1;-4) B(3;2)
Ta có \(\overrightarrow{AB}=\left(2;6\right)\)
=> (d) nhận \(\overrightarrow{AB}=\left(2;6\right)\) làm vtcp
=> (d) có vtpt \(\overrightarrow{n}=\left(-6;2\right)\)
(d) \(\left\{{}\begin{matrix}quaB\left(3;2\right)\\vtpt\overrightarrow{n}=\left(-6;2\right)\end{matrix}\right.\) => pt (d) : -6(x-3) + 2(y-2) hay -6x +2y+14 =0
c)(d) đi qua điểm A(3;-1) và có hệ số góc k=-2
y = k(x-x0) + y0 = -2( x-3) -1
=> y= -2x + 6 -1 => 2x + y +5 =0
viết phương trình tổng quát của đường thẳng Δ biết:
a) Δ đi qua M(-2;3) và có VTPT \(\overrightarrow{n}\)=(1;-4)
Δ \(\left\{{}\begin{matrix}quaM\left(-2;3\right)\\\overrightarrow{n}=\left(1;-4\right)\end{matrix}\right.\) => pt Δ : 1(x+2) -4 (y-3) hay x - 4y +14 =0
b) Δ đi qua M(2;4) và N (5;8)
Ta có \(\overrightarrow{MN}=\left(3;4\right)\)
=> Δ nhận \(\overrightarrow{MN}=\left(3;4\right)\) làm vtcp
=> Δ có vtpt : \(\overrightarrow{n}=\left(-4;3\right)\)
Δ \(\left\{{}\begin{matrix}quaM\left(2;4\right)\\\overrightarrow{n}=\left(-4;3\right)\end{matrix}\right.\) => pt Δ : -4(x-2) + 3(y-4) hay -4x + 3y - 12 = 0
c) giống câu c bài 1
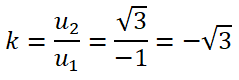
Đáp án: C
Ta có:
Mà: