Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

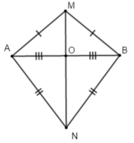
Ta có: MA = MB nên M thuộc đường trung trực của đoạn thẳng AB
Tương tự NA = NB nên N thuộc đường trung trực của đoạn thẳng AB
Suy ra MN là đường trung trực của đoạn thẳng AB
Mà O là trung điểm của AB
Vậy MN vuông góc với AB tại O.
Chọn đáp án C

a. M là trung điểm của AN => AM = MN
N là trung điểm của MB => MN = NB
=> AM = MN = NB
Ta có AB = AM + MN + NB
=> AB = 3MN
b. I là trung điểm của MN => MI = IN
Ta có AI = AM + MI
BI = BN + IN
Mà AM = BN (theo câu a)
IM = IN (cmt)
=> AI = BI
=> I là trung điểm của AB
Chúc bạn học tốt!

Bài 1: Đề như đã sửa thì cách giải như sau:
Trong Tam giác ABC
Có AM/AB = AN/AC
Suy ra: MN // BC .
Trong tam giác ABI
có
MK // BI do K thuộc MN
Do đó : MK/BI =AM/AB (1)
Tương tự trong tam giác AIC
Có NK// IC nên NK/IC = AN/AC (2)
Từ (1) (2) có NK/IC = MK/BI do AN/AC = AM/AB
Lại có IC = IB ( t/c trung tuyến)
nên NK = MK (ĐPCM)
Bài 2:
Bài này thứ tự câu hỏi hình như ngược mình giải lần lượt các câu b) d) c) a)
Từ A kẻ đường cao AH ( H thuộc BC).
b) Do tam giác ABC vuông tại A áp dụng pitago ta có
BC=căn(AB mũ 2 + AC mũ 2)= 20cm
d) Có S(ABC)= AB*AC/2= AH*BC/2
Suy ra: AH= AB*AC/ BC = 12*16/20=9.6 cm
c) Ap dung định lý cosin trong tam giác ABD và ADC ta lần lượt có đẳng thức:
BD^2= AB^2 + AD^2 - 2*AB*AD* cos (45)
DC^2= AC^2+ AD^2 - 2*AC*AD*cos(45) (2)
Trừ vế với vế có:
BD^2-DC^2=AB^2-AC^2- 2*AB*AD* cos (45)+2*AC*AD*cos(45)
(BC-DC)^2-DC^2 = -112+4*Căn (2)* AD.
400-40*DC= -112+................
Suy 128- 10*DC= Căn(2) * AD (3)
Thay (3) v ào (2): rính được DC = 80/7 cm;
BD= BC - DC= 60/7 cm;
a) Ta có S(ABD)=AH*BD/2
S(ADC)=AH*DC/2
Suy ra: S(ABD)/S(ACD)= BD/DC = 60/80=3/4;

Xét tứ giác ABCD có:
+ O là trung điểm AC (gt).
+ O là trung điểm BD (gt).
=> Tứ giác ABCD là hình bình hành (dhnb).
=> BC = AD (Tính chất hình bình hành).
Mà AD = DN (D là trung điểm AN).
=> BC = DN.
Vì tứ giác ABCD là hình bình hành (cmt).
=> BC // AD (Tính chất hình bình hành).
Xét tứ giác DBCN có:
+ BC = DN (cmt).
+ BC // DN (do BC // AD).
=> Tứ giác DBCN là hình bình hành (dhnb).
=> CN // BD (Tính chất hình bình hành). (1)
Vì tứ giác ABCD là hình bình hành (cmt).
=> AB = DC (Tính chất hình bình hành).
Mà AB = BM (B là trung điểm AM).
=> BM = DC.
Vì tứ giác ABCD là hình bình hành (cmt).
=> AB // DC (Tính chất hình bình hành).
Xét tứ giác BMCD có:
+ BM = DC (cmt).
+ BM // CD ( do AB // DC).
=> Tứ giác BMCD là hình bình hành (dhnb).
=> CM // BD. (Tính chất hình bình hành). (2)
Từ (1) và (2) => 3 điểm M, C, N thẳng hàng (đpcm).

ta có:AM:2=BM:3 => 3.AM=2.BM=> AM=2:3.BM
và AB= AM+BM hay AB=2:3BM+BM = 5:3.AM
=> BM= AB:5:3 =AB.3:5
=> BM=15.3:5 = 9
=> AM= 15-9=6
<=> 3AM = 2MB
<=> 3AM - 2MB = 0
ta có: AM + MB = 15
Giải hệ: \(\hept{\begin{cases}3AM-2MB=0\\AM+MB=15\end{cases}}\)
Tìm được. AM = 6, MB = 9
Nhớ bấm L I K E cho mk nhá :))))
