Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
S 8 = n 2 . 2. u 1 + ( n − 1 ) d ⇔ 72 = 8 2 . 2. u 1 + ( 8 − 1 ) . ( − 2 ) ⇔ 72 = 4. ( 2 u 1 − 14 ) ⇔ 2 u 1 − 14 = 18 ⇔ 2 u 1 = 32 ⇔ u 1 = 16
Chọn đáp án A

\(\left\{{}\begin{matrix}u_1=a\\u_{n+1}=\frac{1}{2}u_n\end{matrix}\right.\)
\(\Rightarrow u_n\) là CSN với công bội \(q=\frac{1}{2}\)
\(\Rightarrow u_n=a.\left(\frac{1}{2}\right)^{n-1}\)
\(\Rightarrow lim\left(u_n\right)=lim\left(\frac{a}{2^{n-1}}\right)=0\)
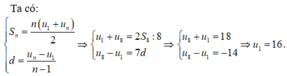
Chọn B
Ta có S 8 = n 2 . [ 2 u 1 + ( n − 1 ) d ]
⇒ 72 = 8 2 . [ 2. u 1 + ( 8 − 1 ) . ( − 2 ) ] ⇔ 72 = 4 . (2u 1 − 14 ) ⇔ 18 = 2 u 1 − 14 ⇔ 2 u 1 = 32 ⇔ u 1 = 16