Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(u_{n+1}=\dfrac{2}{3}u_n+\dfrac{2}{3}\Rightarrow u_{n+1}-2=\dfrac{2}{3}\left(u_n-2\right)\)
Đặt \(u_n-2=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-2=1\\v_{n+1}=\dfrac{2}{3}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(q=\dfrac{2}{3}\Rightarrow v_n=1.\left(\dfrac{2}{3}\right)^{n-1}=\left(\dfrac{2}{3}\right)^{n-1}\)
\(\Rightarrow u_n=v_n+2=\left(\dfrac{2}{3}\right)^{n-1}+2\)

\(u_{n+1}=\dfrac{3}{2}\left(u_n-\dfrac{n+4}{\left(n+1\right)\left(n+2\right)}\right)=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}+\dfrac{2}{n+2}\right)\)
\(\Leftrightarrow u_{n+1}-\dfrac{3}{n+1+1}=\dfrac{3}{2}\left(u_n-\dfrac{3}{n+1}\right)\)
Đặt \(u_n-\dfrac{3}{n+1}=v_n\Rightarrow\left\{{}\begin{matrix}v_1=u_1-\dfrac{3}{2}=-\dfrac{1}{2}\\v_{n+1}=\dfrac{3}{2}v_n\end{matrix}\right.\)
\(\Rightarrow v_n\) là CSN với công bội \(\dfrac{3}{2}\)
\(\Rightarrow v_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}\)
\(\Rightarrow u_n=-\dfrac{1}{2}\left(\dfrac{3}{2}\right)^{n-1}+\dfrac{3}{n+1}\)

Đáp án D
Xét u 2018 v 2018 = S 2018 - S 2017 T 2018 - T 2017 = 3 5

Phương pháp:
Ứng với mỗi giá trị của n = 1, n = 2 ta tính các giá trị u2, u3 rồi tính giá trị của biểu thức.
Cách giải:
Ta có:
u n + 1 = u n + n , u 1 = 3
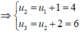
![]()
Chọn B

Từ công thức dãy số ta thấy \(u_n\) là cấp số cộng với \(\left\{{}\begin{matrix}u_1=2\\d=3\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=2+\left(n-1\right)3=3n-1\)
\(\Rightarrow I=\lim\limits\dfrac{3n-1}{3n+1}=1\)