Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:1
- Dãy số u n được gọi là bị chặn nếu nó vừa bị chặn trên, vừa bị chặn dưới, nghĩa là: tồn tại số m, M sao cho m ≤ u n ≤ M , ∀ n ∈ ℕ *
Chú ý: Nếu lim u n = ± ∞ thì ta kết luận ngay dãy không bị chặn.
Cách giải:
Đáp án A: 0 < u n = 2 n + 1 n + 1 = 2 n + 1 − 1 n + 1 = 2 − 1 n + 1 < 2 , ∀ n ∈ ℕ * nên u n là dãy bị chặn.
Đáp án B, C, D: lim u n = + ∞ nên các dãy số này đều không là dãy bị chặn.

Đáp án B
lim n → + ∞ 2 n + 1 n − 1 = 2 do đó dãy số này bị chặn.

Xét đáp án A ta có:
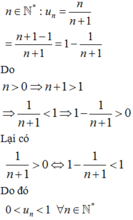
Vậy dãy số u n = n n + 1 là dãy số bị chặn.
Chọn A.

Đáp án D
Các dãy số (hữu hạn hoặc vô hạn) với số hạng tổng quát có dạng an+b ( a, b là hằng số) đều là một cấp số cộng với công sai d = a


Đáp án C
Ta có u n = n n + 1 = 1 − 1 n + 1 < 1 ; u n > 0 do đó dãy số u n = n n + 1 là dãy số nào bị chặn

Đáp án B
Dãy số u n được gọi là dãy số tăng nếu với mọi số tự nhiên n : u n + 1 > u n

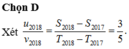
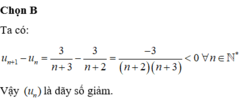
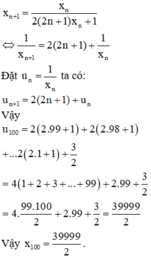
Đáp án D