Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta chứng minh ABEC là hình bình hành mà có Â = 900 Þ tứ giác ABEC là hình chữ nhật.
b) Áp dụng định lý về đường trung bình của tam giác △ A D C ⇒ F G = 1 2 A D = 2 c m
c) Để tứ giác ABEC là hình vuông thì AB = AC ÞDABC phải là tam giác vuông cân tại A.

a) Ta có AD = 1 2 B C = 8 2 = 4 c m
Xét DADC có GF là đường trung bình
⇒ G F = 1 2 A D = 4 2 = 2 c m
b) Chứng minh ADCE là hình thoi. Để ADCE là hình vuông thì điều kiện cần và đủ là E C D ^ = 90 0 ⇔ C 1 ^ = C 2 ^ = 45 0
Û DABC vuông tại A.
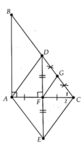

a) Xét ΔAMF có
AE là đường cao ứng với cạnh MF(\(AE\perp MF\))
AE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔAMF cân tại A(Định lí tam giác cân)
hay AM=AF(1)
Xét ΔCFM có
CE là đường cao ứng với cạnh MF(\(CE\perp MF\))
CE là đường trung tuyến ứng với cạnh MF(E là trung điểm của MF)
Do đó: ΔCFM cân tại C(Định lí tam giác cân)
hay CM=CF(2)
Vì ΔABC vuông tại A(gt) có AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{BC}{2}\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(CM=BM=\dfrac{BC}{2}\)(M là trung điểm của BC)
nên AM=CM=BM(3)
Từ (1), (2) và (3) suy ra AM=AF=CF=CM=BM
Xét tứ giác AMCF có AM=CM=CF=FA(cmt)
nên AMCF là hình thoi(Dấu hiệu nhận biết hình thoi)
b)
Sửa đề: Tìm điều kiện của ΔABC để tứ giác AMCF là hình vuông
Hình thoi AMCF trở thành hình vuông khi \(\widehat{AMC}=90^0\)
hay \(AM\perp BC\)
Xét ΔABC có
AM là đường cao ứng với cạnh BC(\(AM\perp BC\))
AM là đường trung tuyến ứng với cạnh BC(M là trung điểm của BC)
Do đó: ΔABC cân tại A(Định lí tam giác cân)
hay AB=AC
Vậy: Khi ΔABC có thêm điều kiện AB=AC thì AMCF trở thành hình vuông
c)
Ta có: MD\(\perp\)AB(gt)
AC\(\perp\)AB(ΔABC vuông tại A)
Do đó: MD//AC(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
MD//AC(cmt)
Do đó: D là trung điểm của AB(Định lí 1 đường trung bình của tam giác)
Xét ΔABC có
M là trung điểm của BC(gt)
D là trung điểm của AB(cmt)
Do đó: MD là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
nên \(MD=\dfrac{AC}{2}\)(Định lí 2 đường trung bình của tam giác)(1)
Ta có: \(ME\perp AC\)(gt)
\(AB\perp AC\)(ΔABC vuông tại A)
Do đó: ME//AB(Định lí 1 từ vuông góc tới song song)
Xét ΔABC có
M là trung điểm của BC(gt)
ME//AB(cmt)
Do đó: E là trung điểm của AC(Định lí 1 đường trung bình của tam giác)
nên \(CE=\dfrac{AC}{2}\)(2)
Từ (1) và (2) suy ra MD=CE
Xét tứ giác CMDE có
MD//CE(MD//AC)
MD=CE(cmt)
Do đó: CMDE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
nên Hai đường chéo CD và EM cắt nhau tại trung điểm của mỗi đường(Định lí hình bình hành)
mà I là trung điểm của EM(gt)
nên I là trung điểm của CD(đpcm)

a: BC=10cm
=>AD=5cm
b: Xet ΔABC có BE/BA=BD/BC
nên ED//AC và ED=AC/2=4cm
=>ED//AF và ED=AF
=>AEDF là hình bình hành
mà góc FAE=90 độ
nên AEDF là hình chữ nhật
c: Xét tứ giá ADBM có
E là trung điểm chung của AB và DM
DA=DB
Do dó: ADBM là hình thoi
\(C_{ADBM}=5\cdot4=20\left(cm\right)\)
d: Để AEDF là hình vuông thì AE=AF
=>AB=AC

Hình bạn tự vẽ
a) Theo định lí Pytago ta có \(BC^2=AB^2+AC^2=100\)
\(\Rightarrow BC=10\left(cm\right)\)
mà BD=DC=> AD=BD=DC\(=\frac{BC}{2}=5\left(cm\right)\)(t/c đường trung tuyến ứng với cạnh huyền)
Theo hệ thức lượng trong tam giác vuông ta có
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{36}+\frac{1}{64}=\frac{25}{576}\)
\(\Rightarrow AH=\frac{24}{5}\left(cm\right)\)
b, Xét tứ giác ABEC có hai đường chéo AE,BC cắt nhau tại trung điểm mỗi đường
=> tứ giác ABEC là hình bình hành
mà \(\widehat{BAC}=90^0\) => tứ giác ABEC là hình chữ nhật

Mình vẽ hình hơi xâu, bạn thông cảm nhé!
a) Xét từ giác ABMC có: + AM cắt BC tại D (bạn dùng ký hiệu giao nhé)
+ DA = DM (gt)
+ DB = DM(gt)
suy ra, tứ giác AMCM là hình bình hành mà ta có góc CAB là góc vuông suy ra tứ giác ABMC là hình chữ nhật
Các câu còn lại bạn đầu có thể giải theo cách trên nhé!
( e mk chưa làm đc, mk mới đc học đến bào hình chữ nhật thôi, sory)
a: Xét tứ giác ABEC có
D là trung điểm của AE
D là trung điểm của BC
Do đó: ABEC là hình bình hành
mà AB=AC
nên ABEC là hình thoi